初中数学圆试题

如图有一个含60°角的直角三角尺，沿其斜边和长直角边中点剪开后，不能拼成
的四边形是（    ）

A．邻边不等的矩形	B．等腰梯形
C．有一角是锐角的菱形	D．正方形

如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC，PF⊥CD，垂足分别为点
E，F，连接AP，EF，给出下列四个结论：
               
①AP =EF；②∠PFE=∠BAP；③PD= EC；④△APD一定是等腰三角形．其中正确的结论有

A．1个

B．2个

C．3个

D．4个

如图，等腰梯形ABCD中，AD∥BC，BD平分∠ABC，∠DBC=30°，AD=5，则BC=

A．5

B．7.5

C．

D．10

如图，在梯形ABCD中，AB∥CD，∠D=90°，AD＝CD＝4，AB=1，F为AD的中点，则F到BC的距离是（ 　 ）．

A．1

B．2

C．4

D．8

如图①在梯形ABCD中，AD∥BC。AB=DC
（1）如果点P，E和F分别是BC，AC和BD的中点，证明：AB=PE＋PF
（2）如果点P是线段BC上任意一点（中点除外），PE∥AB，PF∥DC，如图②所示，那么AB=PE＋PF这个结论还成立吗？请说明理由
（3）如果点P在线段BC的延长线上， PE∥AB，PF∥DC，其他条件不变，那么结论AB=PE＋PF是否成立？直接写出结论，不必证明。

如图，丹东防汛指挥部发现鸭绿江边一处长500米高10米背水坡的坡角为45°的防洪大堤（横断面为梯形ABCD）急需加固，经调查论证，防洪指挥部专家组指定的加固方案是：沿背水坡面用土石进行加固，并使上底加宽3米，加固后背水坡EF的坡比i=1：
（1）求加固后坝底增加的宽度AF
（2）求完成这项工程需要土石多少立方米？（结果保留根号）

如图，点E是平行四边形ABCD的边CD上的一点，连接AE交BC的延长线于点F，要使S_{四边形ABCE} =8S_△CEF ，需要添加一个条件是 

如图，在梯形ABCD中，AD∥BC，BD⊥DC，∠C=60°，AD=4，BC=6，则AB长为

A．2

B．

C．5

D．2

如图，在菱形ABCD 中，AC与BD相较于点O，点P是AB的中点，PO=3，则菱形
ABCD的周长是      .

如图，四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点．若四
边形EFGH为菱形，则对角线AC、BD应满足条件是 
            
A.  AC⊥BD         B. AC=BD       C. AC⊥BD且AC=BD     D. 不确定

如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．
求证：四边形OCED是菱形．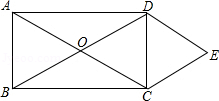

如图，四边形ABCD是平行四边形，点E在边BC上，如果点F是边AD上的点，那么△CDF与△ABE不一定全等的条件是【   】

A．DF=BE

B．AF=CE

C．CF=AE

D．CF∥AE

如图，把长为2cm的正方形剪成四个全等的直角三角形，请用这四个直角三角形（全部用上）拼成下列符合要求的图形（互不重叠且没有空隙），并把你的拼法画在下列的方格纸内（方格为1cm×1cm）

（1）画一个不是正方形的菱形； （2）画一个不是正方形的矩形

（3）画一个不是矩形也不是菱形的平行四边形  （4）画一个梯形 

如图，在矩形ABCD中，AB=2BC，N为DC的中点，点M在DC上，且AM=AB，则∠MBN的度数为      ．

如图，在正方形ABCD中，△APD是正三角形，则∠BPC=