如图所示,点 , , 对应的刻度分别为1,3,5,将线段 绕点 按顺时针方向旋转,当点 首次落在矩形 的边 上时,记为点 ,则此时线段 扫过的图形的面积为

| A. |
|
B. |
6 |
C. |
|
D. |
|
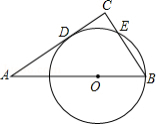
如图,在 中, , ,点 在 上, ,以 为半径的 与 相切于点 ,交 于点 ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
1 |
如图,点 , , , 均在 上,直径 ,点 是 的中点,点 关于 对称的点为 ,若 ,则弦 的长是

| A. |
|
B. |
2 |
C. |
|
D. |
1 |
如图,在菱形 中,对角线 交于点O, , ,以点O为圆心, 长为半径画弧,分别与菱形的边相交,则图中阴影部分的面积为 .(结果保留π)

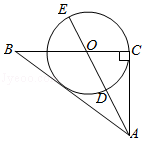
如图,已知AB是⊙O的直径,⊙O经过 的直角边DC上的点F,交AC边于点E,点F是弧EB的中点, ,连接AF.
(1)求证:直线CD是⊙O切线.
(2)若 , ,求 的值.

古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的圆”,请研究如下美丽的圆,如图, 中, , , ,点O在线段 上,且 ,以O为圆心. 为半径的 交线段AO于点D,交线段AO的延长线于点E.
(1)求证: 是 的切线;
(2)研究过短中,小明同学发现 ,回答小明同学发现的结论是否正确?如果正确,给出证明;如果不正确,说明理由.
如图,在 中, , ,点C是 的中点,以OC为半径作 .
(1)求证: 是 的切线;
(2)若 ,求 的长.

如图, 内接于 , 平分 交 边于点 ,交 于点 ,过点 作 于点 ,设 的半径为 , .
(1)过点 作直线 ,求证: 是 的切线;
(2)求证: ;
(3)设 ,求 的值(用含 的代数式表示).

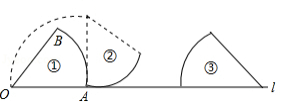
如图,放置在直线 上的扇形 .由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径 , ,则点 所经过的运动路径的长是
A. B. C. D.
如图,在 中, ,以 为直径的 分别交 、 于点 、 ,点 在 的延长线上,且 .
(1)求证: 是 的切线;
(2)若 的直径为4, ,求 .

如图,在 中, ,对角线 , 经过点 , ,与 交于点 ,连接 并延长与 交于点 ,与 的延长线交于点 , .
(1)求证: 是 的切线;
(2)若 ,求 的长(结果保留 .
