初中数学矩形的判定与性质试题

如图，在 $\mathit{\Delta ABC}$ 中， $\mathit{BC}=120$ ，高 $\mathit{AD}=60$ ，正方形 $\mathit{EFGH}$ 一边在 $\mathit{BC}$ 上，点 $E$ ， $F$ 分别在 $\mathit{AB}$ ， $\mathit{AC}$ 上， $\mathit{AD}$ 交 $\mathit{EF}$ 于点 $N$ ，则 $\mathit{AN}$ 的长为 $($ 　　 $)$

A．

15

B．

20

C．

25

D．

30

在中，，，，，分别是，，的中点，连接，．

（1）求证：四边形是矩形；

（2）请用无刻度的直尺在图中作出的平分线（保留作图痕迹，不写作法）．

操作体验：如图，在矩形中，点、分别在边、上，将矩形沿直线折叠，使点恰好与点重合，点落在点处．点为直线上一动点（不与、重合），过点分别作直线、的垂线，垂足分别为点和，以、为邻边构造平行四边形．

（1）如图1，求证：；

（2）特例感知：如图2，若，，当点在线段上运动时，求平行四边形的周长；

（3）类比探究：若，．

①如图3，当点在线段的延长线上运动时，试用含、的式子表示与之间的数量关系，并证明；

②如图4，当点在线段的延长线上运动时，请直接用含、的式子表示与之间的数量关系．（不要求写证明过程）

（1）如图1，在平行四边形ABCD中，∠A＝30°，AB＝6，AD＝8，将平行四边形ABCD分割成两部分，然后拼成一个矩形，请画出拼成的矩形，并说明矩形的长和宽．（保留分割线的痕迹）

（2）若将一边长为1的正方形按如图2﹣1所示剪开，恰好能拼成如图2﹣2所示的矩形，则m的值是多少？

（3）四边形ABCD是一个长为7，宽为5的矩形（面积为35），若把它按如图3﹣1所示的方式剪开，分成四部分，重新拼成如图3﹣2所示的图形，得到一个长为9，宽为4的矩形（面积为36）．问：重新拼成的图形的面积为什么会增加？请说明理由．

如图，在平面直角坐标系中，与轴的正半轴交于、两点，与轴的正半轴相切于点，连接、，已知半径为2，，双曲线经过圆心．

（1）求双曲线的解析式；

（2）求直线的解析式．

如图，在矩形纸片 $\mathit{ABCD}$ 中，将 $\mathit{AB}$ 沿 $\mathit{BM}$ 翻折，使点 $A$ 落在 $\mathit{BC}$ 上的点 $N$ 处， $\mathit{BM}$ 为折痕，连接 $\mathit{MN}$ ；再将 $\mathit{CD}$ 沿 $\mathit{CE}$ 翻折，使点 $D$ 恰好落在 $\mathit{MN}$ 上的点 $F$ 处， $\mathit{CE}$ 为折痕，连接 $\mathit{EF}$ 并延长交 $\mathit{BM}$ 于点 $P$ ，若 $\mathit{AD}=8$ ， $\mathit{AB}=5$ ，则线段 $\mathit{PE}$ 的长等于 　　．

如图，在中，已知，，点为边的中点，连结，过点作于点，将沿直线翻折到的位置．若，则　　．

（1）如图1，有一个残缺圆，请作出残缺圆的圆心（保留作图痕迹，不写作法）．

（2）如图2，设是该残缺圆的直径，是圆上一点，的角平分线交于点，过作的切线交的延长线于点．

①求证：；

②若，，求残缺圆的半圆面积．

如图，在四边形 $\mathit{ABCD}$ 中， $\mathit{AB}//\mathit{DC}$ ， $\angle \mathit{ADC}=90°$ ， $\mathit{AB}=5$ ， $\mathit{CD}=\mathit{AD}=3$ ，点 $E$ 是线段 $\mathit{CD}$ 的三等分点，且靠近点 $C$ ， $\angle \mathit{FEG}$ 的两边与线段 $\mathit{AB}$ 分别交于点 $F$ 、 $G$ ，连接 $\mathit{AC}$ 分别交 $\mathit{EF}$ 、 $\mathit{EG}$ 于点 $H$ 、 $K$ ．若 $\mathit{BG}=\frac{3}{2}$ ， $\angle \mathit{FEG}=45°$ ，则 $\mathit{HK}=($ 　　 $)$

A．

$\frac{2\sqrt{2}}{3}$

B．

$\frac{5\sqrt{2}}{6}$

C．

$\frac{3\sqrt{2}}{2}$

D．

$\frac{13\sqrt{2}}{6}$

如图，在边长为1的菱形中，，将沿射线的方向平移得到△，分别连接，，，则的最小值为　　．

如图，四边形中，对角线、相交于点，，，且．

（1）求证：四边形是矩形；

（2）若，求的度数．

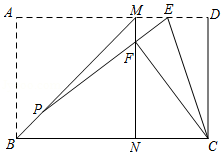
如图，在平行四边形中，点是的中点，点是边上的点，，平行四边形的面积为，由、、三点确定的圆的周长为．

（1）若的面积为30，直接写出的值；

（2）求证：平分；

（3）若，，，求的值．

如图，边长为4的正方形外切于，切点分别为、、、．则图中阴影部分的面积为　　．

如图，抛物线与轴交于、两点（点在点的左侧），与轴交于点，连接、．点沿以每秒1个单位长度的速度由点向点运动，同时，点沿以每秒2个单位长度的速度由点向点运动，当一个点停止运动时，另一个点也随之停止运动，连接．过点作轴，与抛物线交于点，与交于点，连接，与交于点．设点的运动时间为秒．

（1）求直线的函数表达式；

（2）①直接写出，两点的坐标（用含的代数式表示，结果需化简）

②在点、运动的过程中，当时，求的值；

（3）试探究在点，运动的过程中，是否存在某一时刻，使得点为的中点？若存在，请直接写出此时的值与点的坐标；若不存在，请说明理由．

如图是某商品的标志图案， $\mathit{AC}$ 与 $\mathit{BD}$ 是 $\odot O$ 的两条直径，首尾顺次连接点 $A$ ， $B$ ， $C$ ， $D$ ，得到四边形 $\mathit{ABCD}$ ．若 $\mathit{AC}=10\mathit{cm}$ ， $\angle \mathit{BAC}=36°$ ，则图中阴影部分的面积为 $($ 　　 $)$

A．

$5\mathit{\pi c}{m}^2$

B．

$10\mathit{\pi c}{m}^2$

C．

$15\mathit{\pi c}{m}^2$

D．

$20\mathit{\pi c}{m}^2$