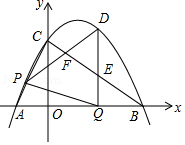
如图,抛物线与轴交于、两点(点在点的左侧),与轴交于点,连接、.点沿以每秒1个单位长度的速度由点向点运动,同时,点沿以每秒2个单位长度的速度由点向点运动,当一个点停止运动时,另一个点也随之停止运动,连接.过点作轴,与抛物线交于点,与交于点,连接,与交于点.设点的运动时间为秒.
(1)求直线的函数表达式;
(2)①直接写出,两点的坐标(用含的代数式表示,结果需化简)
②在点、运动的过程中,当时,求的值;
(3)试探究在点,运动的过程中,是否存在某一时刻,使得点为的中点?若存在,请直接写出此时的值与点的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
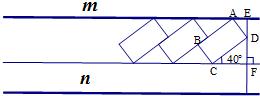
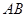 为
为 的直径,
的直径, 为弦,且
为弦,且 ,垂足为
,垂足为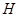 .
.
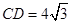 ,求
,求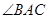 的度数;
的度数; 距离为3的点有多少个?并说明理由.
距离为3的点有多少个?并说明理由.



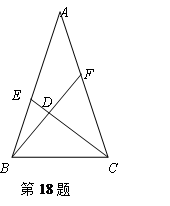
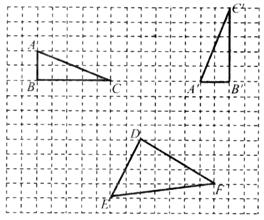
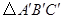 是由格点
是由格点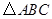 通过怎样变换得到的?
通过怎样变换得到的?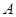 的坐标为(
的坐标为( ,
,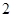 ),点
),点 的坐标为
的坐标为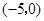 ,请求出过
,请求出过 各顶点的坐标.
各顶点的坐标. 粤公网安备 44130202000953号
粤公网安备 44130202000953号