初中数学矩形的性质解答题

如图，在矩形中，点，在对角线．请添加一个条件，使得结论“”成立，并加以证明．

如图1，已知在平面直角坐标系中，四边形是矩形，点，分别在轴和轴的正半轴上，连结，，，是的中点．

（1）求的长和点的坐标；

（2）如图2，是线段上的点，，点是线段上的一个动点，经过，，三点的抛物线交轴的正半轴于点，连结交于点．

①将沿所在的直线翻折，若点恰好落在上，求此时的长和点的坐标；

②以线段为边，在所在直线的右上方作等边，当动点从点运动到点时，点也随之运动，请直接写出点运动路径的长．

如图，已知正方形的边长为1，正方形的面积为，点在边上，点在的延长线上，设以线段和为邻边的矩形的面积为，且．

（1）求线段的长；

（2）若点为边的中点，连接，求证：．

如图：在平面直角坐标系中，直线与轴交于点，经过点的抛物线的对称轴是．

（1）求抛物线的解析式；

（2）平移直线经过原点，得到直线，点是直线上任意一点，轴于点，轴于点，若点在线段上，点在线段的延长线上，连接，，且．求证：；

（3）若（2）中的点坐标为，点是轴上的点，点是轴上的点，当时，抛物线上是否存在点，使四边形是矩形？如果存在，请求出点的坐标，如果不存在，请说明理由．

在平面直角坐标系中，为原点，点，点在轴的正半轴上，．矩形的顶点，，分别在，，上，．

（Ⅰ）如图①，求点的坐标；

（Ⅱ）将矩形沿轴向右平移，得到矩形，点，，，的对应点分别为，，，．设，矩形与重叠部分的面积为．

①如图②，当矩形与重叠部分为五边形时，，分别与相交于点，，试用含有的式子表示，并直接写出的取值范围；

②当时，求的取值范围（直接写出结果即可）．

在平面直角坐标系中，四边形是矩形，点，点，点．以点为中心，顺时针旋转矩形，得到矩形，点，，的对应点分别为，，．

（Ⅰ）如图①，当点落在边上时，求点的坐标；

（Ⅱ）如图②，当点落在线段上时，与交于点．

①求证；

②求点的坐标．

（Ⅲ）记为矩形对角线的交点，为的面积，求的取值范围（直接写出结果即可）．

综合与实践

问题情境：在数学活动课上，老师出示了这样一个问题：如图1，在矩形中，，是延长线上一点，且，连接，交于点，以为一边在的左下方作正方形，连接．试判断线段与的位置关系．

探究展示：勤奋小组发现，垂直平分，并展示了如下的证明方法：

证明：，．

，．

四边形是矩形，．

．（依据

，．．

即是的边上的中线，

又，．（依据

垂直平分．

反思交流：

（1）①上述证明过程中的“依据1”“依据2”分别是指什么？

②试判断图1中的点是否在线段的垂直平分线上，请直接回答，不必证明；

（2）创新小组受到勤奋小组的启发，继续进行探究，如图2，连接，以为一边在的左下方作正方形，发现点在线段的垂直平分线上，请你给出证明；

探索发现：

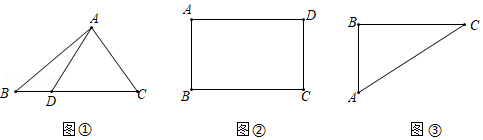
（3）如图3，连接，以为一边在的右上方作正方形，可以发现点，点都在线段的垂直平分线上，除此之外，请观察矩形和正方形的顶点与边，你还能发现哪个顶点在哪条边的垂直平分线上，请写出一个你发现的结论，并加以证明．

综合与实践

背景阅读 早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于我国古代著名数学著作《周髀算经》中，为了方便，在本题中，我们把三边的比为的三角形称为，4，型三角形，例如：三边长分别为9，12，15或，，的三角形就是，4，型三角形，用矩形纸片按下面的操作方法可以折出这种类型的三角形．

实践操作 如图1，在矩形纸片中，，．

第一步：如图2，将图1中的矩形纸片沿过点的直线折叠，使点落在上的点处，折痕为，再沿折叠，然后把纸片展平．

第二步：如图3，将图2中的矩形纸片再次折叠，使点与点重合，折痕为，然后展平，隐去．

第三步：如图4，将图3中的矩形纸片沿折叠，得到△，再沿折叠，折痕为，与折痕交于点，然后展平．

问题解决

（1）请在图2中证明四边形是正方形．

（2）请在图4中判断与的数量关系，并加以证明；

（3）请在图4中证明，4，型三角形；

探索发现

（4）在不添加字母的情况下，图4中还有哪些三角形是，4，型三角形？请找出并直接写出它们的名称．

问题提出

（1）如图①，已知直线及外一点，试在直线上确定、两点，使，并画出这个．

问题探究

（2）如图②，是边长为28的正方形的对称中心，是边上的中点，连接．试在正方形的边上确定点，使线段和将正方形分割成面积之比为的两部分．求点到点的距离．

问题解决

（3）如图③，有一个矩形花园，，．根据设计要求，点、在对角线上，且，并在四边形区域内种植一种红色花卉，在矩形内其他区域均种植一种黄色花卉．已知种植这种红色花卉每平方米需210元，种植这种黄色花卉每平方米需180元．试求按设计要求，完成这两种花卉的种植至少需费用多少元？（结果保留整数．参考数据：，

如图，在中，，是的外接圆，点在上，且，过点作的垂线，与的延长线相交于点，并与的延长线相交于点．

（1）求证：是的切线；

（2）若的半径，，求的长．

问题提出

（1）如图①，已知 $\mathit{\Delta ABC}$ ，请画出 $\mathit{\Delta ABC}$ 关于直线 $\mathit{AC}$ 对称的三角形．

问题探究

（2）如图②，在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=4$ ， $\mathit{AD}=6$ ， $\mathit{AE}=4$ ， $\mathit{AF}=2$ ，是否在边 $\mathit{BC}$ 、 $\mathit{CD}$ 上分别存在点 $G$ 、 $H$ ，使得四边形 $\mathit{EFGH}$ 的周长最小？若存在，求出它周长的最小值；若不存在，请说明理由．

问题解决

（3）如图③，有一矩形板材 $\mathit{ABCD}$ ， $\mathit{AB}=3$ 米， $\mathit{AD}=6$ 米，现想从此板材中裁出一个面积尽可能大的四边形 $\mathit{EFGH}$ 部件，使 $\angle \mathit{EFG}=90°$ ， $\mathit{EF}=\mathit{FG}=\sqrt{5}$ 米， $\angle \mathit{EHG}=45°$ ，经研究，只有当点 $E$ 、 $F$ 、 $G$ 分别在边 $\mathit{AD}$ 、 $\mathit{AB}$ 、 $\mathit{BC}$ 上，且 $\mathit{AF}<\mathit{BF}$ ，并满足点 $H$ 在矩形 $\mathit{ABCD}$ 内部或边上时，才有可能裁出符合要求的部件，试问能否裁得符合要求的面积尽可能大的四边形 $\mathit{EFGH}$ 部件？若能，求出裁得的四边形 $\mathit{EFGH}$ 部件的面积；若不能，请说明理由．

问题提出

（1）如图①，在 $\mathit{\Delta ABC}$ 中， $\mathit{BC}=6$ ， $D$ 为 $\mathit{BC}$ 上一点， $\mathit{AD}=4$ ，则 $\mathit{\Delta ABC}$ 面积的最大值是 　　．

问题探究

（2）如图②，已知矩形 $\mathit{ABCD}$ 的周长为12，求矩形 $\mathit{ABCD}$ 面积的最大值．

问题解决

（3）如图③， $\mathit{\Delta ABC}$ 是葛叔叔家的菜地示意图，其中 $\mathit{AB}=30$ 米， $\mathit{BC}=40$ 米， $\mathit{AC}=50$ 米，现在他想利用周边地的情况，把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地，用来建鱼塘．已知葛叔叔欲建的鱼塘是四边形 $\mathit{ABCD}$ ，且满足 $\angle \mathit{ADC}=60°$ ．你认为葛叔叔的想法能否实现？若能，求出这个四边形鱼塘周长的最大值；若不能，请说明理由．

某校拟建一个面积为 $100m^2$ 的矩形健身区，张老师请同学们小组合作设计出使周长最小的建造方案，下面是其中一个小组的探究过程，请补充完整

（1）列式

设矩形的一边长是 $\mathit{xm}$ ，则另一边长是 　　 $m$ ，若周长为 $\mathit{ym}$ ，则 $y$ 与 $x$ 之间的函数关系式为 　　

（2）画图

①列表

$x$	$\dots$	4	6	10	13	16	20	25	30	$\dots$
$y$	$\dots$	58	$45\frac{1}{3}$	40	$41\frac{5}{13}$	$44\frac{1}{2}$	$a$	58	$66\frac{2}{3}$	$\dots$

表中 $a=$ 　　

②描点：如图所示；

③连线：请在图中画出该函数的图象．

（3）发现

图象最低点的坐标为 　　，即当 $x=$ 　　 $m$ 时，周长 $y$ 有最小值 $40m$ ；

（4）验证

在张老师的指导下，同学们将 $y$ 与 $x$ 之间的函数关系式进行配方，得出 $y=2{(\sqrt{x}-\frac{10}{\sqrt{x}})}^2+40$ ．

$\because 2{(\sqrt{x}-\frac{10}{\sqrt{x}})}^2⩾0$

$\therefore y⩾$ 　　．

$\therefore$ 当 $\sqrt{x}-\frac{10}{\sqrt{x}}=0$ 时， $y$ 有最小值；

此方程可化为 ${\left(\sqrt{x}\right)}^2-10=0$ ；

$\therefore$ 当 $x=$ 　　 $m$ 时，周长 $y$ 有最小值 $40m$ ．

如图，在中，，，．点从点出发，沿向终点运动，同时点从点出发，沿射线运动，它们的速度均为每秒5个单位长度，点到达终点时，、同时停止运动．当点不与点、重合时，过点作于点，连结，以、为邻边作．设与重叠部分图形的面积为，点的运动时间为秒．

（1）①的长为　　；

②的长用含的代数式表示为　　．

（2）当为矩形时，求的值；

（3）当与重叠部分图形为四边形时，求与之间的函数关系式；

（4）当过点且平行于的直线经过一边中点时，直接写出的值．

如图，在矩形中，，．，两点分别从，同时出发，点沿折线运动，在上的速度是，在上的速度是；点在上以的速度向终点运动，过点作，垂足为点．连接，以，为邻边作．设运动的时间为，与矩形重叠部分的图形面积为

（1）当时，　　；

（2）求关于的函数解析式，并写出的取值范围；

（3）直线将矩形的面积分成两部分时，直接写出的值．