如图,矩形中,
,
,点
是对角线
的中点,过点
的直线分别交
、
边于点
、
.
(1)求证:四边形是平行四边形;
(2)当时,求
的长.

如图,在中,
是斜边
的中点,以
为直径作圆
交
于点
,延长
至
,使
,连接
、
,
交圆
于点
.
(1)判断四边形的形状,并说明理由;
(2)求证:;
(3)若,
,求
的长.

如图,将沿着
边翻折,得到
,且
.
(1)判断四边形的形状,并说明理由;
(2)若,
,求四边形
的面积.

如图,已知在中,
,
,
分别是
,
,
的中点,连结
,
,
.
(1)求证:四边形是平行四边形;
(2)若,
,求四边形
的周长.

如图,在平面直角坐标系中,点在抛物线
上,且横坐标为1,点
与点
关于抛物线的对称轴对称,直线
与
轴交于点
,点
为抛物线的顶点,点
的坐标为
.
(1)求线段的长;
(2)点为线段
上方抛物线上的任意一点,过点
作
的垂线交
于点
,点
为
轴上一点,当
的面积最大时,求
的最小值;
(3)在(2)中,取得最小值时,将
绕点
顺时针旋转
后得到△
,过点
作
的垂线与直线
交于点
,点
为抛物线对称轴上的一点,在平面直角坐标系中是否存在点
,使以点
,
,
,
为顶点的四边形为菱形,若存在,请直接写出点
的坐标,若不存在,请说明理由.

如图,是以
为底的等腰三角形,
是边
上的高,点
、
分别是
、
的中点.
(1)求证:四边形是菱形;
(2)如果四边形的周长为12,两条对角线的和等于7,求四边形
的面积
.

将一个直角三角形纸片放置在平面直角坐标系中,点
,点
,点
.
是边
上的一点(点
不与点
,
重合),沿着
折叠该纸片,得点
的对应点
.
(1)如图①,当点在第一象限,且满足
时,求点
的坐标;
(2)如图②,当为
中点时,求
的长;
(3)当时,求点
的坐标(直接写出结果即可).

请阅读下列材料,并完成相应的任务:
在数学中,利用图形在变化过程中的不变性质,常常可以找到解决问题的办法.著名美籍匈牙利数学家波利亚在他所著的《数学的发现》一书中有这样一个例子:请问如何在一个三角形 第一步,在 则有 下面是该结论的部分证明: 证明: 又
同理可得
|
任务:(1)请根据上面的操作步骤及部分证明过程,判断四边形的形状,并加以证明;
(2)请再仔细阅读上面的操作步骤,在(1)的基础上完成的证明过程;
(3)上述解决问题的过程中,通过作平行线把四边形放大得到四边形
,从而确定了点
,
的位置,这里运用了下面一种图形的变化是 .
.平移
.旋转
.轴对称
.位似
综合与实践
问题情境
在综合与实践课上,老师让同学们以"菱形纸片的剪拼"为主题开展数学活动,如图1,将一张菱形纸片 沿对角线 剪开,得到 和 .
操作发现
(1)将图1中的 以 为旋转中心,按逆时针方向旋转角 ,使 ,得到如图2所示的△ ,分别延长 和 交于点 ,则四边形 的形状是 ;
(2)创新小组将图1中的 以 为旋转中心,按逆时针方向旋转角 ,使 ,得到如图3所示的△ ,连接 , ,得到四边形 ,发现它是矩形,请你证明这个结论;
实践探究
(3)缜密小组在创新小组发现结论的基础上,量得图3中 , ,然后提出一个问题:将△ 沿着射线 方向平移 ,得到△ ,连接 , ,使四边形 恰好为正方形,求 的值,请你解答此问题;
(4)请你参照以上操作,将图1中的 在同一平面内进行一次平移,得到△ ,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.

图①,图②均为的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段
,在图②中已画出线段
,其中
、
、
、
均为格点,按下列要求画图:
(1)在图①中,以为对角线画一个菱形
,且
,
为格点;
(2)在图②中,以为对角线画一个对边不相等的四边形
,且
,
为格点,
.

如图①,是矩形
的对角线,
,
.将
沿射线
方向平移到△
的位置,使
为
中点,连接
,
,
,
,如图②.
(1)求证:四边形是菱形;
(2)四边形的周长为 ;
(3)将四边形沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.

如图,在四边形中,
,
,对角线
,
交于点
,
平分
,过点
作
交
的延长线于点
,连接
.
(1)求证:四边形是菱形;
(2)若,
,求
的长.

如图,在四边形中,
为一条对角线,
,
,
,
为
的中点,连接
.
(1)求证:四边形为菱形;
(2)连接,若
平分
,
,求
的长.

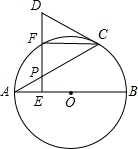
如图, 是 的直径,点 是弦 上一动点(不与 , 重合),过点 作 ,垂足为 ,射线 交 于点 ,交过点 的切线于点 .
(1)求证: ;
(2)若 ,当 是 的中点时,判断以 , , , 为顶点的四边形是什么特殊四边形?说明理由.
(年贵州省贵阳市)如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)