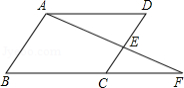
如图,点 是 的边 上的一点,且 ,连接 并延长交 的延长线于点 ,若 , ,则 的周长为

A.21B.28C.34D.42
若 和 均为等腰三角形,且 .
(1)如图(1),点 是 的中点,判定四边形 的形状,并说明理由;
(2)如图(2),若点 是 的中点,连接 并延长至点 ,使 .
求证:① ,
② .

如图,四边形 是一张平行四边形纸片,其高 ,底边 , ,沿虚线 将纸片剪成两个全等的梯形,若 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 是面积为 的 内任意一点, 的面积为 , 的面积为 ,则

A. B.
C. D. 的大小与 点位置有关
如图,在 中, 为 的中点,连接 并延长交 的延长线于点 ,连接 , ,若 ,求证:四边形 是矩形.

如图,点 是 的边 的中点,连结 并延长,交 的延长线于点 .
(1)若 的长为2,求 的长.
(2)若 ,试添加一个条件,并写出 的度数.
如图,在 的网格中, 的三个顶点都在格点上.
(1)在图1中画出一个以 为边的 ,使顶点 , 在格点上.
(2)在图2中画出一条恰好平分 周长的直线 (至少经过两个格点).

如图,已知在平面直角坐标系 中,抛物线 的顶点为 ,与 轴的交点为 .过点 的直线 与抛物线交于另一点 (点 在对称轴左侧),点 在 的延长线上,连结 , , 和 .
(1)如图1,当 轴时,
①已知点 的坐标是 ,求抛物线的解析式;
②若四边形 是平行四边形,求证: .
(2)如图2,若 , ,是否存在这样的点 ,使四边形 是平行四边形?若存在,求出点 的坐标;若不存在,请说明理由.

七巧板是我国祖先的一项卓越创造,流行于世界各地.由边长为2的正方形可以制作一副中国七巧板或一副日本七巧板,如图1所示.分别用这两副七巧板试拼如图2中的平行四边形或矩形,则这两个图形中,中国七巧板和日本七巧板能拼成的个数分别是

A.1和1B.1和2C.2和1D.2和2
在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片 沿过点 的直线折叠,使得点 落在 上的点 处.折痕为 ;再将 , 分别沿 , 折叠,此时点 , 落在 上的同一点 处.请完成下列探究:
(1) 的大小为 ;
(2)当四边形 是平行四边形时, 的值为 .

如图,在 中, , , 的平分线交 于点 ,交 的延长线于点 , 于点 ,若 ,则 的周长为

A.16B.17C.24D.25
如图,四边形 是平行四边形, ,且分别交对角线 于点 , ,连接 , .
(1)求证: ;
(2)若 ,求证:四边形 为菱形.

如图, 的顶点 在等边 的边 上,点 在 的延长线上, 为 的中点,连接 .若 , ,则 的长为 .
