如图,在 中, ,以该三角形的三条边为边向形外作正方形,正方形的顶点 , , , , , 都在同一个圆上.记该圆面积为 , 面积为 ,则 的值是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形 中, , ,点 为 上一点,把 沿 翻折,点 恰好落在 边上的 处,则 的长是
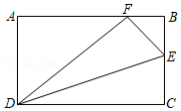
| A. |
1 |
B. |
|
C. |
|
D. |
|
如图,在菱形 中, ,点 , 分别在边 , 上, , 的周长为 ,则 的长为
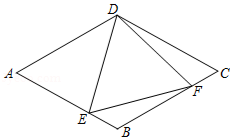
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 中, , , ,将 沿 翻折,使点 与点 重合,则 的长为

| A. |
|
B. |
2 |
C. |
|
D. |
|
《九章算术》中一道"引葭赴岸"问题:"今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?"题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇 生长在它的中央,高出水面部分 为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部 恰好碰到岸边的 处(如图),水深和芦苇长各多少尺?则该问题的水深是 尺.

如图,在 中, , , ,按下列步骤作图:
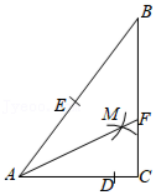
步骤1:以点 为圆心,小于 的长为半径作弧分别交 、 于点 、 .
步骤2:分别以点 、 为圆心,大于 的长为半径作弧,两弧交于点 .
步骤3:作射线 交 于点 .则 的长为
| A. |
6 |
B. |
|
C. |
|
D. |
|
如图,沿 方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从 上的一点 取 , , .那么另一边开挖点 离 多远正好使 , , 三点在一直线上 取1.732,结果取整数)?

在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形 的边为斜边,向内作四个全等的直角三角形,使四个直角顶点 , , , 都是格点,且四边形 为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形 的边长为 ,此时正方形 的面积为5.问:当格点弦图中的正方形 的边长为 时,正方形 的面积的所有可能值是 (不包括 .

如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为
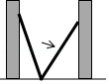
A.0.7米B.1.5米C.2.2米D.2.4米
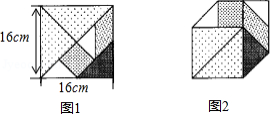
七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是 .
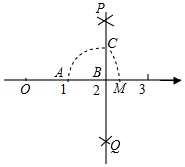
如图,数轴上点 , 分别对应1,2,过点 作 ,以点 为圆心, 长为半径画弧,交 于点 ,以原点 为圆心, 长为半径画弧,交数轴于点 ,则点 对应的数是
A. B. C. D.
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为 ,较短直角边长为 .若 ,大正方形的面积为25,则小正方形的边长为

A.9B.6C.4D.3
如图,数轴上点 对应的数为2, 于 ,且 ,以 为圆心, 长为半径作弧,交数轴于点 ,则 长为
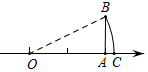
A.3B. C. D.
如图是一块圆环形玉片的残片,作外圆的弦 与内圆相切于点 ,量得 、点 与 的中点 的距离 .则此圆环形玉片的外圆半径为 .
