把两个同样大小的含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点 ,且另三个锐角顶点 , , 在同一直线上.若 ,则 .

把两个同样大小的含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点 ,且另三个锐角顶点 , , 在同一直线上.若 ,则 .
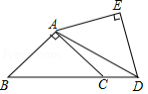
如图,已知 ,以 为直角边作等腰直角三角形 ,再以 为直角边作等腰直角三角形 ,如此下去,则线段 的长度为 .

如图,在矩形 中, , , 是 边的中点, 是 边上的动点,将 沿 所在直线折叠,得到△ ,连接 ,则 的最小值是 .
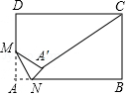
如图,在正方形 中,点 , 分别在 , 上, , 与 相交于点 .下列结论:① 垂直平分 ;② ;③当 时, 为等边三角形;④当 时, .其中正确的是

A.①③B.②④C.①③④D.②③④
我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里 米,则该沙田的面积为
A.7.5平方千米B.15平方千米C.75平方千米D.750平方千米
《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示, 中, , , ,求 的长,如果设 ,则可列方程为 .
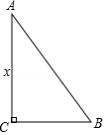
如图,在 中, , 边上的高为4,在 的内部作一个矩形 ,使 在 边上,另外两个顶点分别在 、 边上,则对角线 长的最小值为 .

如图,点 , 在半圆的直径 上,点 , 在 上,四边形 为正方形.若半圆的半径为 ,则正方形的边长为 .

如图,在正方形 内作 , 交 于点 , 交 于点 ,连接 ,过点 作 ,垂足为 ,将 绕点 顺时针旋转 得到 ,若 , ,则 的长为 .

如图,矩形 中, , , 且 与 之间的距离为3,则 的长是
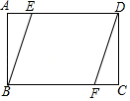
A. B. C. D.
如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足 图形个数有( )

A.1B.2C.3D.4