在四边形 中, , , , .以 为腰作等腰 ,使 ,过点 作 交直线 于点 .请画出图形,并直接写出 的长.
如图,已知线段 , 是 的中点,直线 经过点 , , 点是直线 上一点,当 为直角三角形时,则 .

如图,在 的网格中,每个小正方形的边长均为1,点 , , 都在格点上,若 是 的高,则 的长为

A. B. C. D.
如图,方格纸中每个小正方形的边长均为1,线段 的两个端点均在小正方形的顶点上.
(1)在图中画出以线段 为一边的矩形 (不是正方形),且点 和点 均在小正方形的顶点上;
(2)在图中画出以线段 为一腰,底边长为 的等腰三角形 ,点 在小正方形的顶点上,连接 ,请直接写出线段 的长.

如图,在 中, , , , 平分 交 于 点, , 分别是 , 上的动点,则 的最小值为
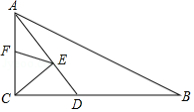
A. B. C. D.6
如图,将沿着
边翻折,得到
,且
.
(1)判断四边形的形状,并说明理由;
(2)若,
,求四边形
的面积.

如图, 为 的直径,弦 ,垂足为点 ,直线 与 的延长线交于点 ,且 .
(1)求证:直线 是 的切线.
(2)若 , ,求线段 的长.

在 中, , , ,若 ,如图1,则有 ;若 为锐角三角形时,小明猜想: ,理由如下:如图2,过点 作 于点 ,设 .在 中, ,在 中,
,
当 为锐角三角形时,
所以小明的猜想是正确的.
(1)请你猜想,当 为钝角三角形时, 与 的大小关系.
(2)温馨提示:在图3中,作 边上的高.
(3)证明你猜想的结论是否正确.

如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形 的面积为20, ,则 的长为

| A. |
4 |
B. |
|
C. |
6 |
D. |
|
)把两个同样大小含角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点
,且另外三个锐角顶点
,
,
在同一直线上.若
,则
.

我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知 , , ,则正方形 的边长是
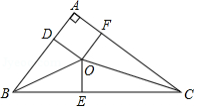
| A. |
|
B. |
2 |
C. |
|
D. |
4 |
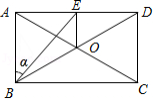
已知:如图,矩形 的对角线 , 相交于点 , , .
(1)求矩形对角线的长;
(2)过 作 于点 ,连结 .记 ,求 的值.
如图,在 中, , , ,点 在线段 上,且 , 是线段 上的一点,连接 ,把四边形 沿直线 翻折,得到四边形 ,当点 恰好落在线段 上时, .
