如图,将两个大小、形状完全相同的 和△ 拼在一起,其中点 与点 重合,点 落在边 上,连接 .若 , ,则 的长为

| A. |
|
B. |
6 |
C. |
|
D. |
|
如图,在正方形 中, .若以 边为底边向其形外作等腰直角 ,连接 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 在 中, , , . 若 是 的中位线, 延长 交 的外角 的平分线于点 ,则线段 的长为

| A. |
A . 7B . 8C . 9D . 10 |
我国古代数学名著《孙子算经》有估算方法:“方五,邪(通“斜” 七.见方求邪,七之,五而一.”译文为:如果正方形的边长为五,则它的对角线长为七.已知正方形的边长,求对角线长,则先将边长乘以七再除以五.若正方形的边长为1,由勾股定理得对角线长为
,依据《孙子算经》的方法,则它的对角线的长是 .
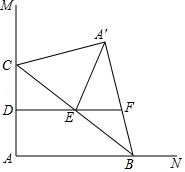
如图,,点
在边
上,
,点
为边
上一动点,连接
,△
与
关于
所在直线对称,点
,
分别为
,
的中点,连接
并延长交
所在直线于点
,连接
.当△
为直角三角形时,
的长为 .
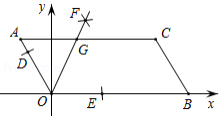
如图,已知的顶点
,
,点
在
轴正半轴上按以下步骤作图:①以点
为圆心,适当长度为半径作弧,分别交边
,
于点
,
;②分别以点
,
为圆心,大于
的长为半径作弧,两弧在
内交于点
;③作射线
,交边
于点
,则点
的坐标为
A.,
B.
,
C.
,
D.
,
如图,在中,
,以
为直径的
交
边于点
,过点
作
,与过点
的切线交于点
,连接
.
(1)求证:;
(2)若,
,求
的长.

我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形 的边 在 轴上, 的中点是坐标原点 ,固定点 , ,把正方形沿箭头方向推,使点 落在 轴正半轴上点 处,则点 的对应点 的坐标为

| A. |
, |
B. |
|
C. |
|
D. |
|
如图,在 中, , , , 垂直平分 交 于点 ,则 的长为

| A. |
6 |
B. |
5 |
C. |
4 |
D. |
3 |
如图,在中,
,
.将
绕点
逆时针旋转一定角度后得到
,其中点
的对应点
落在边
上,则图中阴影部分的面积是 .

如图,在矩形中,
,
,
为边
上一点,
,连接
.动点
、
从点
同时出发,点
以
的速度沿
向终点
运动;点
以
的速度沿折线
向终点
运动.设点
运动的时间为
,在运动过程中,点
,点
经过的路线与线段
围成的图形面积为
.
(1)
,
;
(2)求关于
的函数解析式,并写出自变量
的取值范围;
(3)当时,直接写出
的值.

如图,在中,
,
,
.点
从点
出发,沿
向终点
运动,同时点
从点
出发,沿射线
运动,它们的速度均为每秒5个单位长度,点
到达终点时,
、
同时停止运动.当点
不与点
、
重合时,过点
作
于点
,连结
,以
、
为邻边作
.设
与
重叠部分图形的面积为
,点
的运动时间为
秒.
(1)①的长为 ;
②的长用含
的代数式表示为 .
(2)当为矩形时,求
的值;
(3)当与
重叠部分图形为四边形时,求
与
之间的函数关系式;
(4)当过点且平行于
的直线经过
一边中点时,直接写出
的值.

如图,在中,
,
,
.
是边
上任意一点,沿
剪开,将
沿
方向平移到
的位置,得到四边形
,则四边形
周长的最小值为 .
