如图是用三块正方形纸片以顶点相连的方式设计的"毕达哥拉斯"图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是

| A. |
1,4,5 |
B. |
2,3,5 |
C. |
3,4,5 |
D. |
2,2,4 |
如图,从笔直的公路 旁一点 出发,向西走 到达 ;从 出发向北走 也到达 .下列说法错误的是

| A. |
从点 向北偏西 走 到达 |
| B. |
公路 的走向是南偏西 |
| C. |
公路 的走向是北偏东 |
| D. |
从点 向北走 后,再向西走 到达 |
如图,在四边形中,
,
,对角线
,
交于点
,
平分
,过点
作
交
的延长线于点
,连接
.
(1)求证:四边形是菱形;
(2)若,
,求
的长.

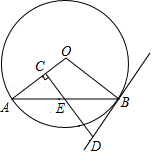
如图,是
的一条弦,
是
的中点,过点
作
于点
,过点
作
的切线交
的延长线于点
.
(1)求证:;
(2)若,
,求
的半径.
如图,在四边形 中, , , , 分别为 , 的中点,连接 , , .
(1)求证: ;
(2) , 平分 , ,求 的长.

如图是一张长方形纸片 ,已知 , , 为 上一点, ,现要剪下一张等腰三角形纸片 ,使点 落在长方形 的某一条边上,则等腰三角形 的底边长是 .

如图,在矩形 中, , ,动点 满足 ,则点 到 、 两点距离之和 的最小值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形纸片中,
,
,点
在
上,将
沿
折叠,点
恰落在边
上的点
处;点
在
上,将
沿
折叠,点
恰落在线段
上的点
处,有下列结论:
①;②
;③
;④
.
其中正确的是 .(把所有正确结论的序号都选上)

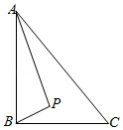
如图, 中, , , , 是 内部的一个动点,且满足 ,则线段 长的最小值为
| A. |
|
B. |
2 |
C. |
|
D. |
|
在中,
,
,
是
的中点.
为直线
上一动点,连接
.过点
作
,交直线
于点
,连接
.
(1)如图1,当是线段
的中点时,设
,
,求
的长(用含
,
的式子表示);
(2)当点在线段
的延长线上时,依题意补全图2,用等式表示线段
,
,
之间的数量关系,并证明.

如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF ②△ABE∽△ACD,③BE+DC>DE④BE2+DC2=DE2,其中正确的有( )个

A.1 B.2 C.3 D.4
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.