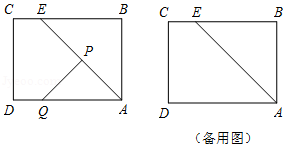
如图,在矩形中,,,为边上一点,,连接.动点、从点同时出发,点以的速度沿向终点运动;点以的速度沿折线向终点运动.设点运动的时间为,在运动过程中,点,点经过的路线与线段围成的图形面积为.
(1) , ;
(2)求关于的函数解析式,并写出自变量的取值范围;
(3)当时,直接写出的值.
推荐套卷
如图,在矩形中,,,为边上一点,,连接.动点、从点同时出发,点以的速度沿向终点运动;点以的速度沿折线向终点运动.设点运动的时间为,在运动过程中,点,点经过的路线与线段围成的图形面积为.
(1) , ;
(2)求关于的函数解析式,并写出自变量的取值范围;
(3)当时,直接写出的值.
