初中数学直角三角形斜边上的中线解答题

如图，已知在中，，，分别是，，的中点，连结，，．

（1）求证：四边形是平行四边形；

（2）若，，求四边形的周长．

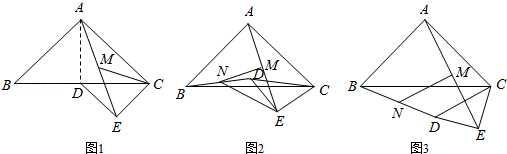
已知 $\mathit{\Delta ABC}$ 是等腰直角三角形， $\angle \mathit{BAC}=90°$ ， $\mathit{CD}=\frac{1}{2}\mathit{BC}$ ， $\mathit{DE}\perp \mathit{CE}$ ， $\mathit{DE}=\mathit{CE}$ ，连接 $\mathit{AE}$ ，点 $M$ 是 $\mathit{AE}$ 的中点．

（1）如图1，若点 $D$ 在 $\mathit{BC}$ 边上，连接 $\mathit{CM}$ ，当 $\mathit{AB}=4$ 时，求 $\mathit{CM}$ 的长；

（2）如图2，若点 $D$ 在 $\mathit{\Delta ABC}$ 的内部，连接 $\mathit{BD}$ ，点 $N$ 是 $\mathit{BD}$ 中点，连接 $\mathit{MN}$ ， $\mathit{NE}$ ，求证： $\mathit{MN}\perp \mathit{AE}$ ；

（3）如图3，将图2中的 $\mathit{\Delta CDE}$ 绕点 $C$ 逆时针旋转，使 $\angle \mathit{BCD}=30°$ ，连接 $\mathit{BD}$ ，点 $N$ 是 $\mathit{BD}$ 中点，连接 $\mathit{MN}$ ，探索 $\frac{\mathit{MN}}{\mathit{AC}}$ 的值并直接写出结果．

如图，是以为底的等腰三角形，是边上的高，点、分别是、的中点．

（1）求证：四边形是菱形；

（2）如果四边形的周长为12，两条对角线的和等于7，求四边形的面积．

如图，在中，，以斜边上的中线为直径作，分别与、交于点、．

（1）过点作的切线与相交于点，求证：；

（2）连接，求证：．

如图1，的直径，是弦上一动点（与点，不重合），，过点作交于点．

（1）如图2，当时，求的长；

（2）如图3，当时，延长至点，使，连接．

①求证：是的切线；

②求的长．

如图，在 $\text{Rt}\Delta \text{ABC}$ 中， $\angle \mathit{ABC}=90°$ ，点 $M$ 是 $\mathit{AC}$ 的中点，以 $\mathit{AB}$ 为直径作 $\odot O$ 分别交 $\mathit{AC}$ ， $\mathit{BM}$ 于点 $D$ ， $E$ ．

（1）求证： $\mathit{MD}=\mathit{ME}$ ；

（2）填空：

①若 $\mathit{AB}=6$ ，当 $\mathit{AD}=2\mathit{DM}$ 时， $\mathit{DE}=$ 　 　；

②连接 $\mathit{OD}$ ， $\mathit{OE}$ ，当 $\angle A$ 的度数为 　 　时，四边形 $\mathit{ODME}$ 是菱形．

如图，在四边形中，为一条对角线，，，，为的中点，连接．

（1）求证：四边形为菱形；

（2）连接，若平分，，求的长．

如图，在四边形 $\mathit{ABCD}$ 中， $\angle \mathit{ABC}=90°$ ， $\mathit{AC}=\mathit{AD}$ ， $M$ ， $N$ 分别为 $\mathit{AC}$ ， $\mathit{CD}$ 的中点，连接 $\mathit{BM}$ ， $\mathit{MN}$ ， $\mathit{BN}$ ．

（1）求证： $\mathit{BM}=\mathit{MN}$ ；

（2） $\angle \mathit{BAD}=60°$ ， $\mathit{AC}$ 平分 $\angle \mathit{BAD}$ ， $\mathit{AC}=2$ ，求 $\mathit{BN}$ 的长．

（年青海省西宁市）如图，CD是△ABC的中线，点E是AF的中点，CF∥AB．

（1）求证：CF=AD；
（2）若∠ACB=90°，试判断四边形BFCD的形状，并说明理由．

（年贵州省遵义市）在Rt△ABC中，∠BAC=,D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F．

（1）求证：△AEF≌△DEB；
（2）证明四边形ADCF是菱形；
（3）若AC=4，AB=5，求菱形ADCFD的面积．