如图,在 中, , , 垂直平分 ,垂足为 ,交 于点 .按以下步骤作图:①以点 为圆心,以适当的长为半径作弧,分别交边 , 于点 , ;②分别以点 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;③作射线 .若 与 的夹角为 ,则 .

如图,在 中, , , 分别是 , 的中点,以 为斜边作 ,若 ,则下列结论不正确的是

A. B. 平分 C. D.
如图,在 中, , ,点 , 分别在 , 上,且 .
(1)如图1,求证: ;
(2)如图2, 是 的中点,求证: ;
(3)如图3, , 分别是 , 的中点,若 , ,求 的面积.

如图,在正方形 中,对角线 与 相交于点 , 为 上一点, , 为 的中点.若 的周长为18,则 的长为 .

如图,在 中, , , ,以点 为圆心, 的长为半径画弧,交 于点 ,交 于点 ,以点 为圆心, 的长为半径画弧,交 于点 ,交 于点 ,则图中阴影部分的面积为
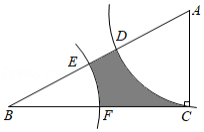
A. B. C. D.
在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形 是矩形, 是 延长线上一点, 是 上一点, , .若 ,则 的度数是
A. B. C. D.
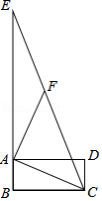
如图,把三角形纸片折叠,使点 、点 都与点 重合,折痕分别为 , ,得到 , ,若 ,则 的长为 .

如图,在 中, , ,将 绕点 旋转得到 △ ,使点 的对应点 落在 上,在 上取点 ,使 ,那么点 到 的距离等于
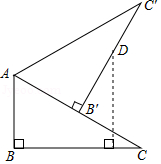
A. B. C. D.
对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点 的斜平移,如点 经1次斜平移后的点的坐标为 ,已知点 的坐标为 .
(1)分别写出点 经1次,2次斜平移后得到的点的坐标.
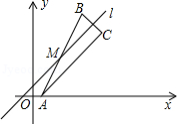
(2)如图,点 是直线 上的一点,点 关于点 的对称点为点 ,点 关于直线 的对称点为点 .
①若 、 、 三点不在同一条直线上,判断 是否是直角三角形?请说明理由.
②若点 由点 经 次斜平移后得到,且点 的坐标为 ,求出点 的坐标及 的值.
如图,在 中, AB AD.

(1)用尺规完成以下基本作图:在 AB上截取 AE,使得 AE= AD;作∠ BCD的平分线交 AB于点 F.(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,连接 DE交 CF于点 P,猜想△ CDP按角分类的类型,并证明你的结论.
已知在平面直角坐标系 中,点 的坐标为 , 是抛物线 对称轴上的一个动点.小明经探究发现:当 的值确定时,抛物线的对称轴上能使 为直角三角形的点 的个数也随之确定,若抛物线 的对称轴上存在3个不同的点 ,使 为直角三角形,则 的值是 .
如图,在 中, , , 的半径为1,点 是 边上的动点,过点 作 的一条切线 (其中点 为切点),则线段 长度的最小值为 .
