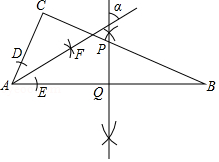
如图，在 中， ， ， 垂直平分 ，垂足为 ，交 于点 ．按以下步骤作图：①以点 为圆心，以适当的长为半径作弧，分别交边 ， 于点 ， ；②分别以点 ， 为圆心，以大于 的长为半径作弧，两弧相交于点 ；③作射线 ．若 与 的夹角为 ，则 ．
相关试题
的最小值为3,则a=
、
、
．．．、a2013中任意四个相邻数之和都是20，已知a4＝2x，a7＝9，a10＝1，
，那么a2013＝．
．
相关知识点
推荐套卷
如图，在 中， ， ， 垂直平分 ，垂足为 ，交 于点 ．按以下步骤作图：①以点 为圆心，以适当的长为半径作弧，分别交边 ， 于点 ， ；②分别以点 ， 为圆心，以大于 的长为半径作弧，两弧相交于点 ；③作射线 ．若 与 的夹角为 ，则 ．
粤公网安备 44130202000953号