初中数学等腰三角形的判定与性质试题

如图， $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$， $\angle \mathit{BAC}=90°$，点 $D$， $E$分别在 $\mathit{AB}$， $\mathit{BC}$上， $\angle \mathit{EAD}=\angle \mathit{EDA}$，点 $F$为 $\mathit{DE}$的延长线与 $\mathit{AC}$的延长线的交点．

（1）求证： $\mathit{DE}=\mathit{EF}$；

（2）判断 $\mathit{BD}$和 $\mathit{CF}$的数量关系，并说明理由；

（3）若 $\mathit{AB}=3$， $\mathit{AE}=\sqrt{5}$，求 $\mathit{BD}$的长．

如图，在 $\mathit{\Delta ABC}$中， $\angle A=36°$， $\mathit{AB}=\mathit{AC}$， $\mathit{BD}$平分 $\angle \mathit{ABC}$，则图中等腰三角形的个数是　　．

如图， $\mathit{\Delta ABC}$的周长为19，点 $D$， $E$在边 $\mathit{BC}$上， $\angle \mathit{ABC}$的平分线垂直于 $\mathit{AE}$，垂足为 $N$， $\angle \mathit{ACB}$的平分线垂直于 $\mathit{AD}$，垂足为 $M$，若 $\mathit{BC}=7$，则 $\mathit{MN}$的长度为 $($　　 $)$

A． $\frac{3}{2}$B．2C． $\frac{5}{2}$D．3

经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形，如果其中一个是等腰三角形，另外一个三角形和原三角形相似，那么把这条线段定义为原三角形的“和谐分割线”．如图，线段 $\mathit{CD}$是 $\mathit{\Delta ABC}$的“和谐分割线”， $\mathit{\Delta ACD}$为等腰三角形， $\mathit{\Delta CBD}$和 $\mathit{\Delta ABC}$相似， $\angle A=46°$，则 $\angle \mathit{ACB}$的度数为　　．

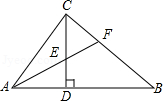
如图，在Rt△ ABC中，∠ ACB＝90°， CD⊥ AB，垂足为 D， AF平分∠ CAB，交 CD于点 E，交 CB于点 F．若 AC＝3， AB＝5，则 CE的长为（　　）

A．

$\frac{3}{2}$

B．

$\frac{4}{3}$

C．

$\frac{5}{3}$

D．

$\frac{8}{5}$

阅读下面的例题及点拨，并解决问题：

例题：如图①，在等边 $\mathit{\Delta ABC}$中， $M$是 $\mathit{BC}$边上一点（不含端点 $B$， $C)$， $N$是 $\mathit{\Delta ABC}$的外角 $\angle \mathit{ACH}$的平分线上一点，且 $\mathit{AM}=\mathit{MN}$．求证： $\angle \mathit{AMN}=60°$．

点拨：如图②，作 $\angle \mathit{CBE}=60°$， $\mathit{BE}$与 $\mathit{NC}$的延长线相交于点 $E$，得等边 $\mathit{\Delta BEC}$，连接 $\mathit{EM}$．易证： $\mathit{\Delta ABM}\cong \mathit{\Delta EBM}\left(\mathit{SAS}\right)$，可得 $\mathit{AM}=\mathit{EM}$， $\angle 1=\angle 2$；又 $\mathit{AM}=\mathit{MN}$，则 $\mathit{EM}=\mathit{MN}$，可得 $\angle 3=\angle 4$；由 $\angle 3+\angle 1=\angle 4+\angle 5=60°$，进一步可得 $\angle 1=\angle 2=\angle 5$，又因为 $\angle 2+\angle 6=120°$，所以 $\angle 5+\angle 6=120°$，即： $\angle \mathit{AMN}=60°$．

问题：如图③，在正方形 $A_1{B}_1{C}_1{D}_1$中， $M_1$是 $B_1{C}_1$边上一点（不含端点 $B_1$， $C_1)$， $N_1$是正方形 $A_1{B}_1{C}_1{D}_1$的外角 $\angle D_1{C}_1{H}_1$的平分线上一点，且 $A_1{M}_1=M_1{N}_1$．求证： $\angle A_1{M}_1{N}_1=90°$．

（1）某学校“智慧方园”数学社团遇到这样一个题目：

如图1，在 $\mathit{\Delta ABC}$中，点 $O$在线段 $\mathit{BC}$上， $\angle \mathit{BAO}=30°$， $\angle \mathit{OAC}=75°$， $\mathit{AO}=3\sqrt{3}$， $\mathit{BO}:\mathit{CO}=1:3$，求 $\mathit{AB}$的长．

经过社团成员讨论发现，过点 $B$作 $\mathit{BD}//\mathit{AC}$，交 $\mathit{AO}$的延长线于点 $D$，通过构造 $\mathit{\Delta ABD}$就可以解决问题（如图 $2)$．

请回答： $\angle \mathit{ADB}=$　　 $°$， $\mathit{AB}=$　　．

（2）请参考以上解决思路，解决问题：

如图3，在四边形 $\mathit{ABCD}$中，对角线 $\mathit{AC}$与 $\mathit{BD}$相交于点 $O$， $\mathit{AC}\perp \mathit{AD}$， $\mathit{AO}=3\sqrt{3}$， $\angle \mathit{ABC}=\angle \mathit{ACB}=75°$， $\mathit{BO}:\mathit{OD}=1:3$，求 $\mathit{DC}$的长．

已知：如图，四边形 $\mathit{ABCD}$是平行四边形，延长 $\mathit{BA}$至点 $E$，使 $\mathit{AE}+\mathit{CD}=\mathit{AD}$．连接 $\mathit{CE}$，求证： $\mathit{CE}$平分 $\angle \mathit{BCD}$．

$\text{Rt}\Delta \text{ABC}$中， $\angle \mathit{ABC}=90°$， $\mathit{AB}=3$， $\mathit{BC}=4$，过点 $B$的直线把 $\mathit{\Delta ABC}$分割成两个三角形，使其中只有一个是等腰三角形，则这个等腰三角形的面积是　　．

（1）【操作发现】

如图1，在边长为1个单位长度的小正方形组成的网格中， $\mathit{\Delta ABC}$ 的三个顶点均在格点上．

①请按要求画图：将 $\mathit{\Delta ABC}$ 绕点 $A$ 顺时针方向旋转 $90°$ ，点 $B$ 的对应点为点 $B\text{'}$ ，点 $C$ 的对应点为点 $C\text{'}$ ．连接 $\mathit{BB}\text{'}$ ；

②在①中所画图形中， $\angle \mathit{AB}\text{'}B=$ 　 　 $°$ ．

（2）【问题解决】

如图2，在 $\text{Rt}\Delta \text{ABC}$ 中， $\mathit{BC}=1$ ， $\angle C=90°$ ，延长 $\mathit{CA}$ 到 $D$ ，使 $\mathit{CD}=1$ ，将斜边 $\mathit{AB}$ 绕点 $A$ 顺时针旋转 $90°$ 到 $\mathit{AE}$ ，连接 $\mathit{DE}$ ，求 $\angle \mathit{ADE}$ 的度数．

（3）【拓展延伸】

如图3，在四边形 $\mathit{ABCD}$ 中， $\mathit{AE}\perp \mathit{BC}$ ，垂足为 $E$ ， $\angle \mathit{BAE}=\angle \mathit{ADC}$ ， $\mathit{BE}=\mathit{CE}=1$ ， $\mathit{CD}=3$ ， $\mathit{AD}=\mathit{kAB}(k$ 为常数），求 $\mathit{BD}$ 的长（用含 $k$ 的式子表示）．

如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED＝150°，则∠A的大小为（　　）

A．150°B．130°C．120°D．100°

如图，在四边形 ABCD中，∠ B＝∠ C＝90°， AB＞ CD， AD＝ AB+ CD．

（1）利用尺规作∠ ADC的平分线 DE，交 BC于点 E，连接 AE（保留作图痕迹，不写作法）；

（2）在（1）的条件下，

①证明： AE⊥ DE；

②若 CD＝2， AB＝4，点 M， N分别是 AE， AB上的动点，求 BM+ MN的最小值．

（1）计算： ${(-1)}^2-{(\pi -2021)}^0+|-\frac{1}{2}|$ ；

（2）如图，在 $\mathit{\Delta ABC}$ 中， $\angle A=40°$ ， $\angle \mathit{ABC}=80°$ ， $\mathit{BE}$ 平分 $\angle \mathit{ABC}$ 交 $\mathit{AC}$ 于点 $E$ ， $\mathit{ED}\perp \mathit{AB}$ 于点 $D$ ，求证： $\mathit{AD}=\mathit{BD}$ ．

如图，已知 $\mathit{AB}=\mathit{AC}$， $\mathit{AD}=\mathit{AE}$， $\mathit{BD}$和 $\mathit{CE}$相交于点 $O$．

（1）求证： $\mathit{\Delta ABD}\cong \mathit{\Delta ACE}$；

（2）判断 $\mathit{\Delta BOC}$的形状，并说明理由．

如图，在矩形 $\mathit{ABCD}$中， $E$是 $\mathit{AB}$边的中点，沿 $\mathit{EC}$对折矩形 $\mathit{ABCD}$，使 $B$点落在点 $P$处，折痕为 $\mathit{EC}$，连接 $\mathit{AP}$并延长 $\mathit{AP}$交 $\mathit{CD}$于 $F$点，连接 $\mathit{CP}$并延长 $\mathit{CP}$交 $\mathit{AD}$于 $Q$点．给出以下结论：

①四边形 $\mathit{AECF}$为平行四边形；

② $\angle \mathit{PBA}=\angle \mathit{APQ}$；

③ $\mathit{\Delta FPC}$为等腰三角形；

④ $\mathit{\Delta APB}\cong \mathit{\Delta EPC}$．

其中正确结论的个数为 $($　　 $)$

A．1B．2C．3D．4