（1）【操作发现】
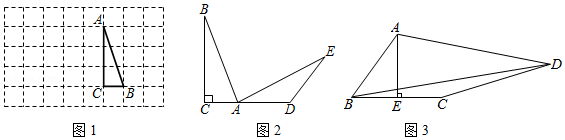
如图1，在边长为1个单位长度的小正方形组成的网格中， 的三个顶点均在格点上．
①请按要求画图：将 绕点 顺时针方向旋转 ，点 的对应点为点 ，点 的对应点为点 ．连接 ；
②在①中所画图形中， ．
（2）【问题解决】
如图2，在 中， ， ，延长 到 ，使 ，将斜边 绕点 顺时针旋转 到 ，连接 ，求 的度数．
（3）【拓展延伸】
如图3，在四边形 中， ，垂足为 ， ， ， ， 为常数），求 的长（用含 的式子表示）．
相关试题
－
=1无解，求m的值。
，再从-2 ， 2，
中选择一个合适的数代入求值.
阅读理解：对于任意正实数a、b，∵(
－
)2≥0，∴a－2
＋b≥0，∴a＋b≥2，只有当a＝b时，等号成立.
结论：在a＋b≥2（a、b均为正实数）中，若ab为定值p，则a+b≥2
，只有当a＝b时，a＋b有最小值2.根据上述内容，回答下列问题：
（1）若m＞0，只有当m＝时，m＋
有最小值；
若m＞0，只有当m＝时，2m＋
有最小值.
（2）如图，已知直线L1：y＝
x＋1与x轴交于点A，过点A的另一直线L2与双曲线y＝
（x>0）相交于点B（2，m），求直线L2的解析式.
（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L1于点D，试
求当线段CD最短时，点A、B、C、D围成的四边形面积.
的图象与一次函数y＝k2x＋b的图象交于A，
，－2)．
推荐套卷
粤公网安备 44130202000953号