初中数学等腰三角形的性质试题

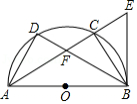
综合与实践

问题情境：

如图①，点 $E$为正方形 $\mathit{ABCD}$内一点， $\angle \mathit{AEB}=90°$，将 $\text{Rt}\Delta \text{ABE}$绕点 $B$按顺时针方向旋转 $90°$，得到 $\mathit{\Delta CBE}\text{'}$（点 $A$的对应点为点 $C)$．延长 $\mathit{AE}$交 $\mathit{CE}\text{'}$于点 $F$，连接 $\mathit{DE}$．

猜想证明：

（1）试判断四边形 $B{E}^{\text{'}}\mathit{FE}$的形状，并说明理由；

（2）如图②，若 $\mathit{DA}=\mathit{DE}$，请猜想线段 $\mathit{CF}$与 $F{E}^{\text{'}}$的数量关系并加以证明；

解决问题：

（3）如图①，若 $\mathit{AB}=15$， $\mathit{CF}=3$，请直接写出 $\mathit{DE}$的长．

等腰三角形的一个内角为 $70°$，则另外两个内角的度数分别是 $($　　 $)$

A． $55°$， $55°$B． $70°$， $40°$或 $70°$， $55°$

C． $70°$， $40°$D． $55°$， $55°$或 $70°$， $40°$

如图， $\mathit{AB}$ 、 $\mathit{BC}$ 、 $\mathit{CD}$ 、 $\mathit{DE}$ 是四根长度均为 $5\mathit{cm}$ 的火柴棒，点 $A$ 、 $C$ 、 $E$ 共线．若 $\mathit{AC}=6\mathit{cm}$ ， $\mathit{CD}\perp \mathit{BC}$ ，则线段 $\mathit{CE}$ 的长度是 $($ 　　 $)$

A．

$6\mathit{cm}$

B．

$7\mathit{cm}$

C．

$6\sqrt{2}\mathit{cm}$

D．

$8\mathit{cm}$

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}$， $\mathit{AO}\perp \mathit{BC}$于点 $O$， $\mathit{OE}\perp \mathit{AB}$于点 $E$，以点 $O$为圆心， $\mathit{OE}$为半径作半圆，交 $\mathit{AO}$于点 $F$．

（1）求证： $\mathit{AC}$是 $\odot O$的切线；

（2）若点 $F$是 $\mathit{OA}$的中点， $\mathit{OE}=3$，求图中阴影部分的面积；

（3）在（2）的条件下，点 $P$是 $\mathit{BC}$边上的动点，当 $\mathit{PE}+\mathit{PF}$取最小值时，直接写出 $\mathit{BP}$的长．

如图，菱形 $\mathit{ABCD}$ 中， $\angle B=60°$ ，点 $P$ 从点 $B$ 出发，沿折线 $\mathit{BC}-\mathit{CD}$ 方向移动，移动到点 $D$ 停止．在 $\mathit{\Delta ABP}$ 形状的变化过程中，依次出现的特殊三角形是 $($ 　　 $)$

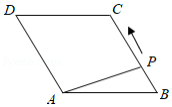
A．	直角三角形 $\to$ 等边三角形 $\to$ 等腰三角形 $\to$ 直角三角形
B．	直角三角形 $\to$ 等腰三角形 $\to$ 直角三角形 $\to$ 等边三角形
C．	直角三角形 $\to$ 等边三角形 $\to$ 直角三角形 $\to$ 等腰三角形
D．	等腰三角形 $\to$ 等边三角形 $\to$ 直角三角形 $\to$ 等腰三角形

如图，在 $▱\mathit{ABCD}$中， $\angle A=70°$， $\mathit{DC}=\mathit{DB}$，则 $\angle \mathit{CDB}=$　　．

若实数 $m$、 $n$满足等式 $|m-2|+\sqrt{n-4}=0$，且 $m$、 $n$恰好是等腰 $\mathit{\Delta ABC}$的两条边的边长，则 $\mathit{\Delta ABC}$的周长是 $($　　 $)$

A．12B．10C．8D．6

已知 $a$ ， $b$ 是等腰三角形的两边长，且 $a$ ， $b$ 满足 $\sqrt{2a-3b+5}+{(2a+3b-13)}^2=0$ ，则此等腰三角形的周长为 $($ 　　 $)$

A．

8

B．

6或8

C．

7

D．

7或8

问题：如图，在 $\mathit{\Delta ABD}$中， $\mathit{BA}=\mathit{BD}$．在 $\mathit{BD}$的延长线上取点 $E$， $C$，作 $\mathit{\Delta AEC}$，使 $\mathit{EA}=\mathit{EC}$．若 $\angle \mathit{BAE}=90°$， $\angle B=45°$，求 $\angle \mathit{DAC}$的度数．

答案： $\angle \mathit{DAC}=45°$．

思考：（1）如果把以上“问题”中的条件“ $\angle B=45°$”去掉，其余条件不变，那么 $\angle \mathit{DAC}$的度数会改变吗？说明理由．

（2）如果把以上“问题”中的条件“ $\angle B=45°$”去掉，再将“ $\angle \mathit{BAE}=90°$”改为“ $\angle \mathit{BAE}=n°$”，其余条件不变，求 $\angle \mathit{DAC}$的度数．

如图，等腰直角三角形 $\mathit{ABC}$中， $\angle \mathit{ABC}=90°$， $\mathit{BA}=\mathit{BC}$，将 $\mathit{BC}$绕点 $B$顺时针旋转 $\theta (0°<\theta <90°)$，得到 $\mathit{BP}$，连结 $\mathit{CP}$，过点 $A$作 $\mathit{AH}\perp \mathit{CP}$交 $\mathit{CP}$的延长线于点 $H$，连结 $\mathit{AP}$，则 $\angle \mathit{PAH}$的度数 $($　　 $)$

A．随着 $\theta$的增大而增大B．随着 $\theta$的增大而减小

C．不变D．随着 $\theta$的增大，先增大后减小

已知：如图，在 $\mathit{\Delta OAB}$中， $\mathit{OA}=\mathit{OB}$， $\odot O$与 $\mathit{AB}$相切于点 $C$．求证： $\mathit{AC}=\mathit{BC}$．小明同学的证明过程如下框：

证明：连结 $\mathit{OC}$， $\because \mathit{OA}=\mathit{OB}$， $\therefore \angle A=\angle B$， 又 $\because \mathit{OC}=\mathit{OC}$， $\therefore \mathit{\Delta OAC}\cong \mathit{\Delta OBC}$， $\therefore \mathit{AC}=\mathit{BC}$．

小明的证法是否正确？若正确，请在框内打“ $\surd$”；若错误，请写出你的证明过程．

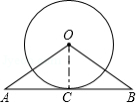
如图，在等腰 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{AC}=2\sqrt{5}$， $\mathit{BC}=8$，按下列步骤作图：

①以点 $A$为圆心，适当的长度为半径作弧，分别交 $\mathit{AB}$， $\mathit{AC}$于点 $E$， $F$，再分别以点 $E$， $F$为圆心，大于 $\frac{1}{2}\mathit{EF}$的长为半径作弧相交于点 $H$，作射线 $\mathit{AH}$；

②分别以点 $A$， $B$为圆心，大于 $\frac{1}{2}\mathit{AB}$的长为半径作弧相交于点 $M$， $N$，作直线 $\mathit{MN}$，交射线 $\mathit{AH}$于点 $O$；

③以点 $O$为圆心，线段 $\mathit{OA}$长为半径作圆．

则 $\odot O$的半径为 $($　　 $)$

A． $2\sqrt{5}$B．10C．4D．5

如图， $\mathit{AB}$是半圆 $O$的直径， $C$， $D$是半圆 $O$上不同于 $A$， $B$的两点， $\mathit{AD}=\mathit{BC}$， $\mathit{AC}$与 $\mathit{BD}$相交于点 $F$． $\mathit{BE}$是半圆 $O$所在圆的切线，与 $\mathit{AC}$的延长线相交于点 $E$．

（1）求证： $\mathit{\Delta CBA}\cong \mathit{\Delta DAB}$；

（2）若 $\mathit{BE}=\mathit{BF}$，求证： $\mathit{AC}$平分 $\angle \mathit{DAB}$．

如图， $\mathit{\Delta ABC}$ 中， $\mathit{AB}=\mathit{AC}=2$ ， $P$ 是 $\mathit{BC}$ 上任意一点， $\mathit{PE}\perp \mathit{AB}$ 于点 $E$ ， $\mathit{PF}\perp \mathit{AC}$ 于点 $F$ ，若 $S_{\mathit{\Delta ABC}}=1$ ，则 $\mathit{PE}+\mathit{PF}=$ 　　．

如图， $\mathit{AD}$是等腰三角形 $\mathit{ABC}$的顶角平分线， $\mathit{BD}=5$，则 $\mathit{CD}$等于 $($　　 $)$

A．10B．5C．4D．3