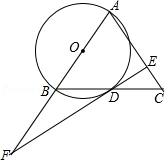
如图,在 中, ,以 为直径作 交 于点 ,过点 作 的切线 交 于点 ,交 延长线于点 .
(1)求证: ;
(2)若 , ,求 的长.
《淮南子 天文训》中记载了一种确定东西方向的方法,大意是:日出时,在地面上点 处立一根杆,在地面上沿着杆的影子的方向取一点 ,使 , 两点间的距离为10步(步是古代的一种长度单位),在点 处立一根杆;日落时,在地面上沿着点 处的杆的影子的方向取一点 ,使 , 两点间的距离为10步,在点 处立一根杆.取 的中点 ,那么直线 表示的方向为东西方向.
(1)上述方法中,杆在地面上的影子所在直线及点 , , 的位置如图所示.使用直尺和圆规,在图中作 的中点 (保留作图痕迹);

(2)在如图中,确定了直线 表示的方向为东西方向.根据南北方向与东西方向互相垂直,可以判断直线 表示的方向为南北方向,完成如下证明.
证明:在 中, , 是 的中点,
(填推理的依据).
直线 表示的方向为东西方向,
直线 表示的方向为南北方向.
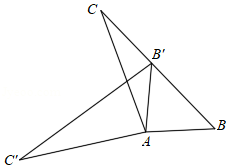
如图,在 中, ,将 绕点 按逆时针方向旋转得到△ .若点 恰好落在 边上,且 ,则 的度数为
| A. |
|
B. |
|
C. |
|
D. |
|
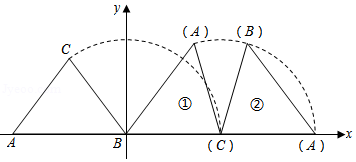
等腰三角形 在平面直角坐标系中的位置如图所示,已知点 ,点 在原点, ,把等腰三角形 沿 轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置② 依此规律,第15次翻转后点 的横坐标是 .
如图,等腰的两个顶点
、
在反比例函数
的图象上,
.过点
作边
的垂线交反比例函数
的图象于点
,动点
从点
出发,沿射线
方向运动
个单位长度,到达反比例函数
图象上一点,则
.

如图,在 中, , ,分别以点 , 为圆心, 的长为半径作弧,两弧交于点 ,连接 , ,则四边形 的面积为

A. B.9C.6D.
函数 的图象与 轴、 轴分别交于 、 两点,点 在 轴上.若 为等腰三角形,则满足条件的点 共有 个.
如图,在 中, 是 边上的点,以 为圆心, 为半径的 与 相切于点 , 平分 , , , 的长是

A. B.2C. D.
如图, 是 的切线,切点为 , 的延长线交 于点 ,若 ,则 的度数为

A. B. C. D.