如图,在中,
,
,
.
(1)尺规作图:不写作法,保留作图痕迹.
①作的平分线,交斜边
于点
;
②过点作
的垂线,垂足为点
.
(2)在(1)作出的图形中,求的长.

如图,在中,
.
(1)已知线段的垂直平分线与
边交于点
,连接
,求证:
.
(2)以点为圆心,线段
的长为半径画弧,与
边交于点
,连接
.若
,求
的度数.

在中,
平分
交
于点
.

(1)如图1,若,
,求
的面积;
(2)如图2,过点作
,交
的延长线于点
,分别交
,
于点
,
,且
.求证:
.
在 中, , ,点 是 上一点,连接 ,过点 作 ,在 上取点 ,连接 .延长 至 ,使 ,连接 , ,且 .
(1)若 ,求 的长;
(2)如图1,当点 在 上时,求证: ;
(3)如图2,当点 在 的垂直平分线上时,直接写出 的值.

如图,在正方形 中,连接 ,以点 为圆心,适当长为半径画弧,交 、 于点 , ,分别以 , 为圆心,大于 长的一半为半径画弧,两弧交于点 ,连结 并延长交 于点 ,再分别以 、 为圆心,以大于 长的一半为半径画弧,两弧交于点 , ,作直线 ,分别交 , , 于点 , , ,交 的延长线于点 ,连接 ,下列结论:① ,② ,③ ,④ .其中正确的是

| A. |
①②③ |
B. |
②③④ |
C. |
①③④ |
D. |
①②④ |
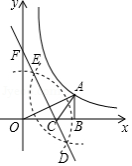
如图,点 在双曲线 上,过点 作 轴,垂足为点 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 交 轴于点 ,交 轴于点 ,连接 .若 ,则 的值为
| A. |
2 |
B. |
|
C. |
|
D. |
|
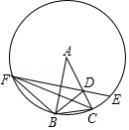
如图, 、 是 上的两点, 的垂直平分线与 交于 、 两点,与线段 交于 点.若 ,则
| A. |
|
B. |
|
C. |
|
D. |
|
已知:如图,、
是
的两条弦,且
,
是
延长线上一点,联结
并延长交
于点
,联结
并延长交
于点
.
(1)求证:;
(2)如果,求证:四边形
是菱形.

已知在平面直角坐标系中(如图),已知抛物线
经过点
,对称轴是直线
,顶点为
.
(1)求这条抛物线的表达式和点的坐标;
(2)点在对称轴上,且位于顶点上方,设它的纵坐标为
,联结
,用含
的代数式表示
的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点在
轴上.原抛物线上一点
平移后的对应点为点
,如果
,求点
的坐标.
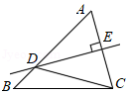
如图,在 中, , .若边 的垂直平分线 交边 于点 ,交边 于点 ,连接 ,则
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在四边形 中, , , , .分别以点 , 为圆心,大于 长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 于点 .若点 是 的中点,则 的长为

| A. |
|
B. |
4 |
C. |
3 |
D. |
|
如图,在 中, ,分别以点 、 为圆心,大于 长为半径画弧,两弧在 两侧分别交于 、 两点,作直线 交 于点 ,交 于点 .若 , ,则 的长为

| A. |
4 |
B. |
6 |
C. |
8 |
D. |
10 |
问题发现
(1)如图(1),四边形 中,若 , ,则线段 , 的位置关系为 ;
拓展探究
(2)如图(2),在 中,点 为斜边 的中点,分别以 , 为底边,在 外部作等腰三角形 和等腰三角形 ,连接 , ,分别交 , 于点 , ,试猜想四边形 的形状,并说明理由;
解决问题
(3)如图(3),在正方形 中, ,以点 为旋转中心将正方形 旋转 ,得到正方形 ,请直接写出 的长度.
