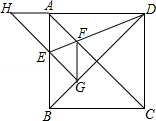
如图,正方形 ABCD的边长为1, AC, BD是对角线.将△ DCB绕着点 D顺时针旋转45°得到△ DGH, HG交 AB于点 E,连接 DE交 AC于点 F,连接 FG.则下列结论:
①四边形 AEGF是菱形
②△ AED≌△ GED
③∠ DFG=112.5°
④ BC+ FG=1.5
其中正确的结论是 .
如图,在 中, , ,点 在斜边 上,以 为直角边作等腰直角三角形 , ,则 , , 三者之间的数量关系是 .

如图,已知正方形 ,点 是边 延长线上的动点(不与点 重合),且 , 由 平移得到,若过点 作 , 为垂足,则有以下结论:
①点 位置变化,使得 时, ;
②无论点 运动到何处,都有 ;
③在点 的运动过程中,四边形 可能成为菱形;
④无论点 运动到何处, 一定大于 .
以上结论正确的有 (把所有正确结论的序号都填上).

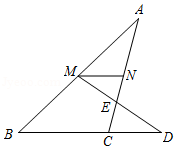
如图,在等边 中, ,点 , 分别在边 , 上,且 ,连接 , 交于点 ,连接 ,则 的最小值是 .

如图,在 中, , , ,以 为圆心,以适当的长为半径作弧,交 于点 ,交 于点 .分别以 , 为圆心,以大于 的长为半径作弧,两弧在 的内部相交于点 ,作射线 ,交 于点 ,点 在 边上, ,连接 ,则 的周长为 .

如图,在 中, , 分别是 和 的中点,连接 ,点 是 的中点,连接 并延长,交 的延长线于点 .若 ,则 的长为 .
如图,在菱形 中, ,点 , 分别在 , 上,且 , 与 相交于点 , 与 相交于点 .下列结论:① ;② ;③若 ,则 ;④ .其中正确的结论有 .(只填序号即可)

如图,在四边形 中, , ,我们把这种两组邻边分别相等的四边形叫做“筝形”.筝形 的对角线 , 相交于点 .以点 为圆心, 长为半径画弧,分别交 , 于点 , .若 , ,则 的长为 (结果保留 .

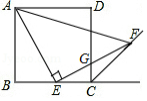
如图,四边形是边长为2的正方形,点
是边
上一动点(不与点
,
重合),
,且
交正方形外角的平分线
于点
,交
于点
,连接
,有下列结论:
①;
②;
③;
④的面积的最大值为1.
其中正确结论的序号是 .(把正确结论的序号都填上)
匈牙利著名数学家爱尔特希.
,
曾提出:在平面内有
个点,其中每三个点都能构成等腰三角形,人们将具有这样性质的
个点构成的点集称为爱尔特希点集.如图,是由五个点
、
、
、
、
构成的爱尔特希点集(它们为正五边形的任意四个顶点及正五边形的中心构成),则
的度数是 .

如图,在中,
,
是
的中点,点
在
上,
,
,垂足分别为
,
,连接
.则下列结论中:
①;
②;
③;
④;
⑤若平分
,则
;
⑥,
正确的有 .(只填序号)
