初中数学全等三角形的判定与性质填空题

如图，在Rt△ ABC中，∠ ABC＝90°， BC＝3， D为斜边 AC的中点，连接 BD，点 F是 BC边上的动点（不与点 B、 C重合），过点 B作 BE⊥ BD交 DF延长线交于点 E，连接 CE，下列结论：

①若 BF＝ CF，则 CE ²+ AD ²＝ DE ²；

②若∠ BDE＝∠ BAC， AB＝4，则 CE＝ $\frac{15}{8}$ ；

③△ ABD和△ CBE一定相似；

④若∠ A＝30°，∠ BCE＝90°，则 DE＝ $\sqrt{21}$ ．

其中正确的是 　．（填写所有正确结论的序号）

如图，在矩形 ABCD中， AB＝8， BC＝6， M为 AD上一点，将△ ABM沿 BM翻折至△ EBM， ME和 BE分别与 CD相交于 O， F两点，且 OE＝ OD，则 AM的长为 　　．

如图，已知正方形 ABCD，点 M是边 BA延长线上的动点（不与点 A重合），且 AM＜ AB，△ CBE由△ DAM平移得到．若过点 E作 EH⊥ AC， H为垂足，则有以下结论：①点 M位置变化，使得∠ DHC＝60°时，2 BE＝ DM；②无论点 M运动到何处，都有 DM＝ $\sqrt{2}$ HM；③无论点 M运动到何处，∠ CHM一定大于135°．其中正确结论的序号为 　　．

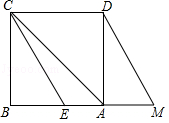
如图1， AF， BE是△ ABC的中线， AF⊥ BE，垂足为点 P，设 BC＝ a， AC＝ b， AB＝ c，则 a ²+ b ²＝5 c ²，利用这一性质计算．如图2，在▱ ABCD中， E， F， G分别是 AD， BC， CD的中点， EB⊥ EG于点 E， AD＝8， AB＝2 $\sqrt{5}$ ，则 AF＝ 　　．

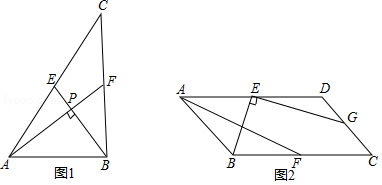
如图，在Rt△ ACB中，∠ ACB＝90°， AC＝ BC， D是 AB上的一个动点（不与点 A， B重合），连接 CD，将 CD绕点 C顺时针旋转90°得到 CE，连接 DE， DE与 AC相交于点 F，连接 AE．下列结论：

①△ ACE≌△ BCD；

②若∠ BCD＝25°，则∠ AED＝65°；

③ DE ²＝2 CF• CA；

④若 AB＝3 $\sqrt{2}$ ， AD＝2 BD，则 AF＝ $\frac{5}{3}$ ．

其中正确的结论是 　　．（填写所有正确结论的序号）

如图，边长为4的正方形ABCD内接于圆O，点E是 $\stackrel{̂}{\mathit{AB}}$上的一动点（不与A、B重合），点F是 $\stackrel{̂}{\mathit{BC}}$上的一点，连接OE、OF，分别与AB、BC交于点G，H，且 $\angle \mathit{EOF}＝90°$，有以下结论：

① $\stackrel{̂}{\mathit{AE}}=\stackrel{̂}{\mathit{BF}}$；

②△OGH是等腰三角形；

③四边形OGBH的面积随着点E位置的变化而变化；

④△GBH周长的最小值为 $4+\sqrt{2}$.

其中正确的是　 　（把你认为正确结论的序号都填上）．

如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是　          ．

（1） $\mathit{EF}=\sqrt{2}\mathit{OE}$；（2） $S_{\mathit{四边形}\mathit{OEBF}}:S_{\mathit{正方形}\mathit{ABCD}}＝1:4$；（3） $\mathit{BE}+\mathit{BF}=\sqrt{2}\mathit{OA}$；（4）在旋转过程中，当△BEF与△COF的面积之和最大时， $\mathit{AE}=\frac{3}{4}$；（5） $\mathit{OG}•\mathit{BD}＝A{E}^2+C{F}^2$．

如图，在▱ ABCD中，∠ B＝30°， AB＝ AC， O是两条对角线的交点，过点 O作 AC的垂线分别交边 AD， BC于点 E， F；点 M是边 AB的一个三等分点，则△ AOE与△ BMF的面积比为 　　．

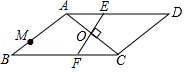
如图， M、 N是正方形 ABCD的边 CD上的两个动点，满足 AM＝ BN，连接 AC交 BN于点 E，连接 DE交 AM于点 F，连接 CF，若正方形的边长为4，则线段 CF的最小值是 　．

如图，在△ ABC与△ ADE中， AB＝ AC， AD＝ AE，∠ BAC＝∠ DAE，且点 D在 AB上，点 E与点 C在 AB的两侧，连接 BE， CD，点 M、 N分别是 BE、 CD的中点，连接 MN， AM， AN．

下列结论：①△ ACD≌△ ABE；②△ ABC∽△ AMN；③△ AMN是等边三角形；④若点 D是 AB的中点，则 S _{△ ABC}＝2 S _{△ ABE}．

其中正确的结论是 　．（填写所有正确结论的序号）

如图，在矩形 ABCD中，点 E是 CD的中点，点 F是 BC上一点，且 FC＝2 BF，连接 AE， EF．若 AB＝2， AD＝3，则cos∠ AEF的值是 　　．

如图，正方形 ABCD的面积为3 cm ²， E为 BC边上一点，∠ BAE＝30°， F为 AE的中点，过点 F作直线分别与 AB， DC相交于点 M， N．若 MN＝ AE，则 AM的长等于 　　 cm．

如图，在四边形中，，是中点，于点，，．

（1）若，则四边形的面积　　；

（2）若，则此时四边形的面积　　（用“”或“”或“”填空）．

如图，在△ABC中，分别以AC、BC为边作等边三角形ACD和等边三角形BCE，连接AE、BD交于点O，则∠AOB的度数为　　．

如图，在Rt△ACB中，∠ACB＝90°，AC＝BC＝3，CD＝1，CH⊥BD于H，点O是AB中点，连接OH，则OH＝　　．