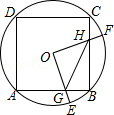
如图,边长为4的正方形ABCD内接于圆O,点E是 上的一动点(不与A、B重合),点F是 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且 ,有以下结论:
① ;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为 .
其中正确的是 (把你认为正确结论的序号都填上).
相关知识点
推荐套卷
如图,边长为4的正方形ABCD内接于圆O,点E是 上的一动点(不与A、B重合),点F是 上的一点,连接OE、OF,分别与AB、BC交于点G,H,且 ,有以下结论:
① ;
②△OGH是等腰三角形;
③四边形OGBH的面积随着点E位置的变化而变化;
④△GBH周长的最小值为 .
其中正确的是 (把你认为正确结论的序号都填上).
