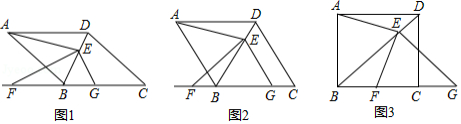
如图,点 , , , 在直线 上 , 之间不能直接测量),点 , 在 异侧,测得 , , .
(1)求证: ;
(2)指出图中所有平行的线段,并说明理由.

如图,在 中, ,点 是斜边 上一点,且 .
(1)作 的平分线,交 于点 ;(要求尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,连接 ,求证: .

如图,已知四边形ABCD中,∠C=∠D=90°,AE平分∠DAB,BE平分∠ABC,且E在D上.
(1)求∠AEB;
(2)求证:DE=CE.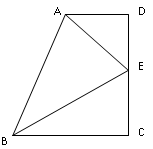
如图,矩形 中,延长 至 ,延长 至 , ,连接 ,与 、 分别相交于 、 两点.
(1)求证: ;
(2)若 , , ,求矩形 的面积.

阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1) 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3.

 求
求 的值;
的值;
 若CD=2,求BP的长.
若CD=2,求BP的长.
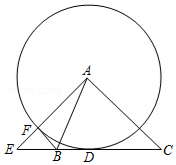
如图, 与 相切于点 ,过点 作 ,垂足为 ,交 于点 .连接 , ,并延长 交 于点 ,与 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的值.

如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
如图, 为等腰直角三角形,延长 至点 使 , 是矩形,其对角线 , 交于点 ,连接 交 于点 .
(1)求证: ;
(2)求 的值.

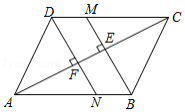
已知:如图,四边形 为平行四边形,点 、 、 、 在同一直线上, .
求证:(1) ;
(2) .

如图,在 中,过 点作 于点 ,交 于点 ,过 点作 于点 ,交 于点 .
(1)求证:四边形 是平行四边形;
(2)已知 , ,求 的长.
在菱形 中,点 为对角线 上一点,点 , 在直线 上,且 , .
(1)如图1,求证: ;
(2)如图2,当 时,求证: ;
(3)如图3,当 ,点 在线段 上时,线段 , , 的数量关系如何?(请直接写出你猜想的结论)