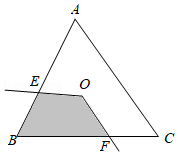
如图, 的顶点 是边长为2的等边 的重心, 的两边与 的边交于 , , ,则 与 的边所围成阴影部分的面积是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在正方形 中, 是 边上的一点, , ,将正方形边 沿 折叠到 ,延长 交 于 ,连接 , ,现在有如下4个结论:
① ;② ;③ ;④ .
其中正确结论的个数是

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
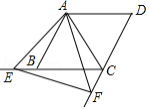
如图,在菱形 中,已知 , , ,点 在 的延长线上,点 在 的延长线上,有下列结论:
① ;② ;③ ;④若 ,则点 到 的距离为 .
则其中正确结论的个数是
| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,一束光线从点 出发,经 轴上的点 反射后经过点 ,则点 的坐标是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在正方形 的对角线 上取一点 .使得 ,连接 并延长 到 ,使 , 与 相交于点 ,若 ,有下列结论:① ;② ;③ ;④ .则其中正确的结论有

| A. |
①②③ |
B. |
①②③④ |
C. |
①②④ |
D. |
①③④ |
如图,有两张矩形纸片 和 , , .把纸片 交叉叠放在纸片 上,使重叠部分为平行四边形,且点 与点 重合.当两张纸片交叉所成的角 最小时, 等于

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, , , 于点 , 于点 , .连接 ,将 沿直线 翻折至 所在的平面内,得 ,连接 .过点 作 交 于点 .则四边形 的周长为

| A. |
8 |
B. |
|
C. |
|
D. |
|
如图,在正方形 中,连接 ,点 是 的中点,若 、 是边 上的两点,连接 、 ,并分别延长交边 于两点 、 ,则图中的全等三角形共有

| A. |
2对 |
B. |
3对 |
C. |
4对 |
D. |
5对 |
如图,在四边形 中, , , , .分别以点 , 为圆心,大于 长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 于点 .若点 是 的中点,则 的长为

| A. |
|
B. |
4 |
C. |
3 |
D. |
|
如图,正方形 的顶点 、 的坐标分别为 , ,则点 关于原点 的对称点的坐标为

| A. |
|
B. |
|
C. |
|
D. |
|
如图, , 平分 ,且 .若点 , 分别在 , 上,且 为等边三角形,则满足上述条件的 有

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
3个以上 |
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF ②△ABE∽△ACD,③BE+DC>DE④BE2+DC2=DE2,其中正确的有( )个

A.1 B.2 C.3 D.4
如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y= (x>0)的图像上,已知点B的坐标是(
(x>0)的图像上,已知点B的坐标是( ,
, ),则k的值为( )
),则k的值为( )

| A.10 | B.8 | C.6 | D.4 |
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,小明在探究筝形的性质时,得到如下结论:

①AC⊥BD;②AO=CO= AC;③△ABD≌△CBD,其中正确的结论有( )
AC;③△ABD≌△CBD,其中正确的结论有( )
| A.①② | B.①③ | C.②③ | D.①②③ |