如图,在 中, , 分别是 , 边上的中线,且 ,垂足为点 ,设 , , ,则下列关系式中成立的是
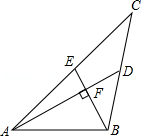
A. B. C. D.
如图,点 为 的重心,连接 , 并延长分别交 , 于点 , ,连接 ,若 , , ,则 的长度为

A.1.7B.1.8C.2.2D.2.4
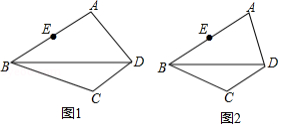
如图,在四边形 中, , , 为 的中点,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
(1)在图1中,画出 的 边上的中线;
(2)在图2中,若 ,画出 的 边上的高.
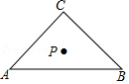
如图,已知在 中, , , ,点 是 的重心,则点 到 所在直线的距离等于
A.1B. C. D.2
如图,直角 中, ,点 是 的重心,连接 并延长交 于点 ,过点 作 交 于点 ,连接 交 于点 ,则 的值为

A. B. C. D.
在 中,已知 和 分别是边 、 上的中线,且 ,垂足为 .若 , ,则线段 的长度为 .
在 中, 、 分别为线段 、 上的点(不与 、 、 重合).
(1)如图1,若 ,求证:
(2)如图2,若 不与 平行,(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若 上一点 恰为 的重心, ,求 的值.

如图所示的网格由边长相同的小正方形组成,点 、 、 、 、 、 、 在小正方形的顶点上,则 的重心是

A.点 B.点 C.点 D.点
阅读材料:三角形的三条中线必交于一点,这个交点称为三角形的重心.

(1)特例感知:如图(一 ,已知边长为2的等边 的重心为点 ,求 与 的面积.
(2)性质探究:如图(二 ,已知 的重心为点 ,请判断 、 是否都为定值?如果是,分别求出这两个定值;如果不是,请说明理由.
(3)性质应用:如图(三 ,在正方形 中,点 是 的中点,连接 交对角线 于点 .
①若正方形 的边长为4,求 的长度;
②若 ,求正方形 的面积.
如图,已知点F是△ABC的重心,连接BF并延长,交AC于点E,连接CF并延长,交AB于点D,过点F作FG∥BC,交AC于点G.设三角形EFG,四边形FBCG的面积分别为S1,S2,则S1:S2= .

给出下列结论:
①三角形的重心是三角形三条边上的中线的交点;
②圆内接四边形的对角相等;
③圆心角为,半径为4的扇形的面积是
;
④在平面直角坐标系中,如果以原点为位似中心画出一个与原图形位似的图形,它与原图形的相似比为3,那么与原图形上的点对应的位似图形上点
的坐标为
或
.
其中正确的结论是 (填写正确结论的编号)
(年云南省昆明市)如图,△ABC是等边三角形,高AD、BE相交于点H,BC= ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
