阅读材料:三角形的三条中线必交于一点,这个交点称为三角形的重心.
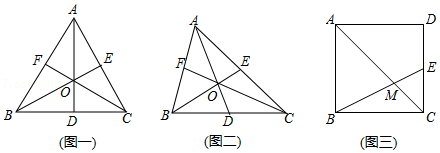
(1)特例感知:如图(一 ,已知边长为2的等边 的重心为点 ,求 与 的面积.
(2)性质探究:如图(二 ,已知 的重心为点 ,请判断 、 是否都为定值?如果是,分别求出这两个定值;如果不是,请说明理由.
(3)性质应用:如图(三 ,在正方形 中,点 是 的中点,连接 交对角线 于点 .
①若正方形 的边长为4,求 的长度;
②若 ,求正方形 的面积.
相关知识点
推荐套卷
阅读材料:三角形的三条中线必交于一点,这个交点称为三角形的重心.

(1)特例感知:如图(一 ,已知边长为2的等边 的重心为点 ,求 与 的面积.
(2)性质探究:如图(二 ,已知 的重心为点 ,请判断 、 是否都为定值?如果是,分别求出这两个定值;如果不是,请说明理由.
(3)性质应用:如图(三 ,在正方形 中,点 是 的中点,连接 交对角线 于点 .
①若正方形 的边长为4,求 的长度;
②若 ,求正方形 的面积.