如图,正方形 中, , 是 边的中点,点 是正方形内一动点, ,连接 ,将线段 绕点 逆时针旋转 得 ,连接 , .

(1)求证: ;
(2)若 , , 三点共线,连接 ,求线段 的长.
(3)求线段 长的最小值.
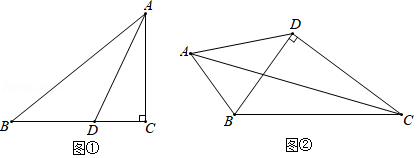
如图,沿 方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从 上的一点 取 , , .那么另一边开挖点 离 多远正好使 , , 三点在一直线上 取1.732,结果取整数)?

如图, 中, , 平分 交 于点 ,按下列步骤作图:
步骤1:分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点;
步骤2:作直线 ,分别交 , 于点 , ;
步骤3:连接 , .
若 , ,则线段 的长为

A. B. C. D.
下列长度的三条线段能组成直角三角形的是
A . 3 , 4 , 5B . 2 , 3 , 4C . 4 , 6 , 7D . 5 , 11 , 12
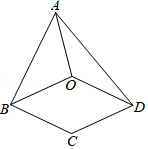
如图,在四边形 中, , . 是四边形 内一点,且 .求证:
(1) ;
(2)四边形 是菱形.
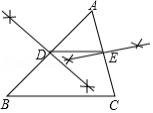
如图,在 中,用直尺和圆规作 、 的垂直平分线,分别交 、 于点 、 ,连接 .若 ,则 .
如图, ,且 . 、 是 上两点, , .若 , , ,则 的长为
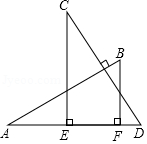
A. B. C. D.
在数学兴趣小组活动中,小亮进行数学探究活动. 是边长为2的等边三角形, 是 上一点,小亮以 为边向 的右侧作等边三角形 ,连接 .
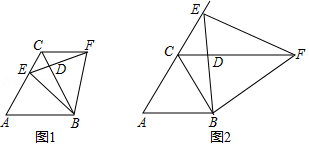
(1)如图1,当点 在线段 上时, 、 相交于点 ,小亮发现有两个三角形全等,请你找出来,并证明.
(2)当点 在线段 上运动时,点 也随着运动,若四边形 的面积为 ,求 的长.
(3)如图2,当点 在 的延长线上运动时, 、 相交于点 ,请你探求 的面积 与 的面积 之间的数量关系.并说明理由.
(4)如图2,当 的面积 时,求 的长.
如图,矩形 中, 是 的中点,延长 , 交于点 ,连接 , .
(1)求证:四边形 是平行四边形;
(2)当 平分 时,写出 与 的数量关系,并说明理由.

如图, 、 , 、 分别为矩形 的边 、 、 、 的中点,连接 、 、 , , .已知 , ,则 的长为 .

如果三角形的两个内角 与 满足 ,那么我们称这样的三角形为“准互余三角形”.
(1)若 是“准互余三角形”, , ,则 ;
(2)如图①,在 中, , , .若 是 的平分线,不难证明 是“准互余三角形”.试问在边 上是否存在点 (异于点 ,使得 也是“准互余三角形”?若存在,请求出 的长;若不存在,请说明理由.
(3)如图②,在四边形 中, , , , ,且 是“准互余三角形”,求对角线 的长.