如图, 和 都是等腰直角三角形, , , , , 为 边中点,连接 ,且 、 、 三点恰好在一条直线上, 交 于点 ,连接 , .
(1)求证: ;
(2)猜想 , , 之间的数量关系,并证明;
(3)若 , ,请写出线段 , 的长.

如图,矩形 中, , ,点 是 边上一点, ,连接 ,点 是 延长线上一点,连接 ,且 ,则 .
如图, 与 , , 分别交于点 , , ,且 , ,则下列结论错误的是

| A. |
|
B. |
|
C. |
|
D. |
|
在 中, , 平分 ,交对角线 于点 ,交射线 于点 ,将线段 绕点 顺时针旋转 得线段 .
(1)如图1,当 时,连接 ,请直接写出线段 和线段 的数量关系;
(2)如图2,当 时,过点 作 于点,连接 ,请写出线段 , , 之间的数量关系,并说明理由;
(3)当 时,连接 ,若 ,请直接写出 与 面积的比值.

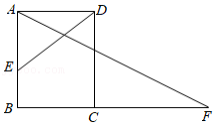
如图,将正方形纸片 沿 折叠,使点 的对称点 落在边 上,点 的对称点为点 , 交 于点 ,连接 交 于点 ,连接 .下列四个结论中:① ;② ;③ 平分 ;④ ,正确的是 (填序号即可).

如图,在 中, ,由图中的尺规作图痕迹得到的射线 与 交于点 ,点 为 的中点,连接 ,若 ,则 的周长为

| A. |
|
B. |
|
C. |
|
D. |
4 |
课本再现
(1)在证明"三角形内角和定理"时,小明只撕下三角形纸片的一个角拼成图1即可证明,其中与 相等的角是 ;

类比迁移
(2)如图2,在四边形 中, 与 互余,小明发现四边形 中这对互余的角可类比(1)中思路进行拼合:先作 ,再过点 作 于点 ,连接 ,发现 , , 之间的数量关系是 ;
方法运用
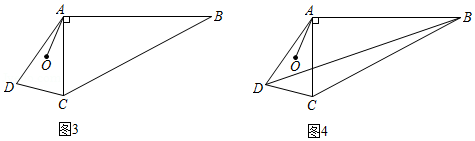
(3)如图3,在四边形 中,连接 , ,点 是 两边垂直平分线的交点,连接 , .
①求证: ;
②连接 ,如图4,已知 , , ,求 的长(用含 , 的式子表示).
如图,正比例函数 的图象与反比例函数 的图象交于点 在 中, , ,点 坐标为 .
(1)求 的值;
(2)求 所在直线的解析式.

如图,在边长为 的正六边形 中,连接 , ,其中点 , 分别为 和 上的动点.若以 , , 为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为 .

在一次数学探究活动中,李老师设计了一份活动单:
已知线段 ,使用作图工具作 ,尝试操作后思考: (1)这样的点 唯一吗? (2)点 的位置有什么特征?你有什么感悟? |
“追梦”学习小组通过操作、观察、讨论后汇报:点 的位置不唯一,它在以 为弦的圆弧上(点 、 除外), .小华同学画出了符合要求的一条圆弧(如图 .
(1)小华同学提出了下列问题,请你帮助解决.
①该弧所在圆的半径长为 ;
② 面积的最大值为 ;
(2)经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形内部,我们记为 ,请你根据图1证明 .
(3)请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形 的边长 , ,点 在直线 的左侧,且 .
①线段 长的最小值为 ;
②若 ,则线段 长为 .
