初中数学三角形填空题

如图，在每个小正方形的边长为1的网格中，点，，均在格点上．

（1）的长等于　　；

（2）在的内部有一点，满足，请在如图所示的网格中，用无刻度的直尺，画出点，并简要说明点的位置是如何找到的（不要求证明）　　．

如图，正方形和正方形的边长分别为3和1，点，分别在边，上，为的中点，连接，则的长为　　．

如图，在每个小正方形的边长为1的网格中， $A$ ， $E$ 为格点， $B$ ， $F$ 为小正方形边的中点， $C$ 为 $\mathit{AE}$ ， $\mathit{BF}$ 的延长线的交点．

（Ⅰ） $\mathit{AE}$ 的长等于 　　；

（Ⅱ）若点 $P$ 在线段 $\mathit{AC}$ 上，点 $Q$ 在线段 $\mathit{BC}$ 上，且满足 $\mathit{AP}=\mathit{PQ}=\mathit{QB}$ ，请在如图所示的网格中，用无刻度的直尺，画出线段 $\mathit{PQ}$ ，并简要说明点 $P$ ， $Q$ 的位置是如何找到的（不要求证明） 　　．

如图，在正方形中，点，，，分别在边，，，上，点，，都在对角线上，且四边形和均为正方形，则的值等于　　．

如图，在中，，，点为内一点，，，连接，将绕点按逆时针方向旋转，使与重合，点的对应点为点，连接，交于点，则的长为　　．

如图，在平面直角坐标中，点为坐标原点，菱形的顶点在轴的正半轴上，点坐标为，点的坐标为，反比例函数的图象恰好经过点，则的值为　　．

如图，在中，，，，点是的中点，以为直径作，分别与，交于点，，过点作的切线，交于点，则的长为　　．

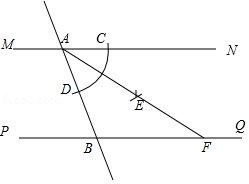
如图，直线，直线分别与，相交于点，．小宇同学利用尺规按以下步骤作图：①以点为圆心，以任意长为半径作弧交于点，交于点；②分别以，为圆心，以大于长为半径作弧，两弧在内交于点；③作射线交于点．若，，则线段的长为　　．

一副三角板按如图方式摆放，得到和，其中，，，为的中点，过点作于点．若，则的长为　　．

如图，已知点为线段的中点，且，连接，，是的平分线，与相交于点，于点，交于点，则的长为　　．

在和△中，已知，，，，点、分别在边、上，且△，那么的长是　　．

如图，已知直线，含角的三角板的直角顶点在上，角的顶点在上，如果边与的交点是的中点，那么　　度．

已知任一平面封闭图形，现在其外部存在一水平放置的矩形，使得矩形每条边都与该图形有至少一个交点，且构成该图形的所有点都在矩形内部或矩形边上，那么就称这个矩形为“该图形的矩形”，且这个矩形的水平长成为该图形的宽，铅直高称为该图形的高．如图，边长为1的菱形的一条边水平放置，已知“该菱形的矩形”的“高”是“宽”的，则该“菱形的矩形”的“宽”为　　．

我们规定：一个正边形为整数，的最短对角线与最长对角线长度的比值叫做这个正边形的“特征值”，记为，那么　　．

如图，已知，，，．分别以点、为圆心画圆．如果点在内，点在外，且与内切，那么的半径长的取值范围是　　．