如图是一张矩形纸片,点 在 边上,把 沿直线 对折,使点 落在对角线 上的点 处,连接 .若点 , , 在同一条直线上, ,则 , .

如图,在 的方格中, 、 、 、 、 、 分别位于格点上,从 、 、 、 四点中任取一点,与点 、 为顶点作三角形,则所作三角形为等腰三角形的概率是 .

如图,在 中, ,以 为直径的 与 交于点 ,与 交于点 ,连 交 于点 ,且 ,则 长为 .
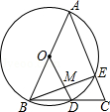
如图1, AF, BE是△ ABC的中线, AF⊥ BE,垂足为点 P,设 BC= a, AC= b, AB= c,则 a 2+ b 2=5 c 2,利用这一性质计算.如图2,在▱ ABCD中, E, F, G分别是 AD, BC, CD的中点, EB⊥ EG于点 E, AD=8, AB=2 ,则 AF= .
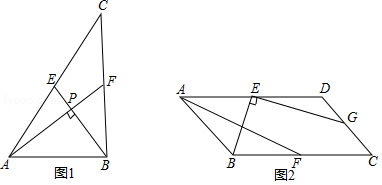
如图,已知正方形 ABCD,点 M是边 BA延长线上的动点(不与点 A重合),且 AM< AB,△ CBE由△ DAM平移得到.若过点 E作 EH⊥ AC, H为垂足,则有以下结论:①点 M位置变化,使得∠ DHC=60°时,2 BE= DM;②无论点 M运动到何处,都有 DM= HM;③无论点 M运动到何处,∠ CHM一定大于135°.其中正确结论的序号为 .
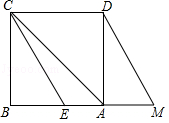
如图,在△ABC中, ,AB的垂直平分线交AB于点E,交BC于点D,连接AD,若 ,则 .

如图,矩形纸片 , , , 为边 上一点.将 沿 所在的直线折叠,点 恰好落在 边上的点 处,过点 作 ,垂足为点 ,取 的中点 ,连接 ,则 .
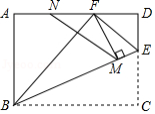
如图,将面积为 的矩形 沿对角线 折叠,点 的对应点为点 ,连接 交 于点 .若 ,则 的长为 .
