初中数学三角形填空题

如图1，四个全等的直角三角形围成一个大正方形，中间是个小正方形，这个图形是我国汉代赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．在此图形中连接四条线段得到如图2的图案，记阴影部分的面积为，空白部分的面积为，大正方形的边长为，小正方形的边长为，若，则的值为　　．

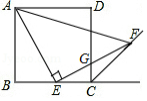
如图，矩形中，为边上一点，将沿折叠，使点的对应点恰好落在边上，连接交于点，连接．若，，则矩形的面积为　　．

在中，若弦垂直平分半径，则弦所对的圆周角等于　　．

如图，在中，，，则　．

如图，四边形是边长为2的正方形，点是边上一动点（不与点，重合），，且交正方形外角的平分线于点，交于点，连接，有下列结论：

①；

②；

③；

④的面积的最大值为1．

其中正确结论的序号是　　．（把正确结论的序号都填上）

在探索数学名题“尺规三等分角”的过程中，有下面的问题：如图，是的对角线，点在上，，，则的大小是　　．

如图，中，点，，分别为，，的中点，点，，分别为，，的中点，若随机向内投一粒米，则米粒落在图中阴影部分的概率为　　．

如图，是等边三角形外一点．若，，连接，则的最大值与最小值的差为　　．

如图，圆心角为的扇形内，以为直径作半圆，连接．若阴影部分的面积为，则　　．

如图，在中，是的垂直平分线．若，的周长为13，则的周长为　　．

已知：，求作：的外接圆．作法：①分别作线段，的垂直平分线和，它们相交于点；②以点为圆心，的长为半径画圆．如图，即为所求，以上作图用到的数学依据有：　

如图所示的扇形 $\mathit{AOB}$ 中， $\mathit{OA}=\mathit{OB}=2$ ， $\angle \mathit{AOB}=90°$ ， $C$ 为 $\stackrel{̂}{\mathit{AB}}$ 上一点， $\angle \mathit{AOC}=30°$ ，连接 $\mathit{BC}$ ，过 $C$ 作 $\mathit{OA}$ 的垂线交 $\mathit{AO}$ 于点 $D$ ，则图中阴影部分的面积为 　　．

匈牙利著名数学家爱尔特希．，曾提出：在平面内有个点，其中每三个点都能构成等腰三角形，人们将具有这样性质的个点构成的点集称为爱尔特希点集．如图，是由五个点、、、、构成的爱尔特希点集（它们为正五边形的任意四个顶点及正五边形的中心构成），则的度数是　　．

如图，直线，点在直线上，点在直线上，，，，则　　．

如图，是的外接圆，，于点，延长交于点，若，，则的长是　 　．