数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形中,
,
.如图,建立平面直角坐标系
,使得边
在
轴正半轴上,点
在
轴正半轴上,则点
的坐标是 .

如图, 为半圆 的直径, , 是半圆上的三等分点, , 与半圆 相切于点 .点 为 上一动点(不与点 , 重合),直线 交 于点 , 于点 ,延长 交 于点 ,则下列结论正确的是 .(写出所有正确结论的序号)
① ;② 的长为 ;③ ;④ ;⑤ 为定值.

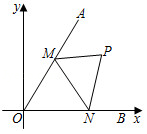
在平面直角坐标系中的位置如图所示,且
,在
内有一点
,
,
分别是
,
边上的动点,连接
,
,
,则
周长的最小值是 .
如图,正比例函数与反比例函数
的图象交于
,
两点,过点
作
轴于点
,过点
作
轴于点
,则
的面积为 .

在平面直角坐标系中,为原点,点
,点
在
轴的正半轴上,
,矩形
的顶点
,
,
分别在
,
,
上,
.将矩形
沿
轴向右平移,当矩形
与
重叠部分的面积为
时,则矩形
向右平移的距离为 .

如图,在矩形中,
,
.分别以点
,
为圆心,以大于
的长为半径画弧,两弧相交于点
和
.作直线
分别与
,
,
交于点
,
,
,则
.

如图1,已知四边形是正方形,将
,
分别沿
,
向内折叠得到图2,此时
与
重合
、
都落在
点),若
,
,则
的长为 .
