数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:

小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
②小聪的作法正确吗?请说明理由.
③请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
如图,已知△ABC,用直尺(没有刻度)和圆规在平面上求作一个点P,使P到∠A两边的距离相等,且PA=PB.(不要求写作法,但要保留作图痕迹)
画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.
(1)尺规作图(不写作法,保留作图痕迹):
作∠AOB的平分线OP;作线段CD的垂直平分线EF,分别与CD、OP相交于E、F;连接OE、CF、DF.
(2)在所画图中,线段OE与CD之间有怎样的数量关系,线段DF与CF之间有怎样的数量关系,并说明理由.
如图所示,要在公园(四边形ABCD)中建造一座音乐喷泉,喷泉位置应符合如下要求: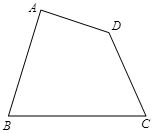
(1)到公园两个出入口A、C的距离相等;
(2)到公园两边围墙AB、AD的距离相等.
请你用尺规作图的方法确定喷泉的位置P.(不必写作法,但要保留作图痕迹)
作图题:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵黄桷树.如图,要求黄桷树的位置点P到边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种黄桷树的位置点P(不写作法,保留作图痕迹).
在一次消防演习中,消防员架起一架25米长的云梯,如图斜靠在一面墙上,梯子底端离墙7米.
(1)求这个梯子的顶端距地面有多高?
(2)如果消防员接到命令,要求梯子的顶端下降4米(云梯长度不变),那么云梯的底部在水平方向应滑动多少米?
(年贵州省贵阳市)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,FO⊥AB,垂足为点O,连接AF并延长交⊙O于点D,连接OD交BC于点E,∠B=30°,FO=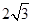 .
.
(1)求AC的长度;
(2)求图中阴影部分的面积.(计算结果保留根号)
(年贵州省毕节)如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.
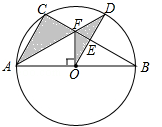
(年云南省昆明市)如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.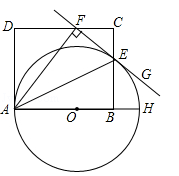
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径.
(年青海省中考)如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.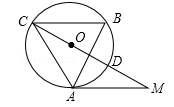
(1)求证:AM=AC;
(2)若AC=3,求MC的长.
(年新疆乌鲁木齐市)如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=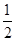 ,AB=3,求BD的长.
,AB=3,求BD的长.