初中数学三角形选择题

如图，边长都为4的正方形 $\mathit{ABCD}$ 和正三角形 $\mathit{EFG}$ 如图放置， $\mathit{AB}$ 与 $\mathit{EF}$ 在一条直线上，点 $A$ 与点 $F$ 重合．现将 $\mathit{\Delta EFG}$ 沿 $\mathit{AB}$ 方向以每秒1个单位的速度匀速运动，当点 $F$ 与 $B$ 重合时停止．在这个运动过程中，正方形 $\mathit{ABCD}$ 和 $\mathit{\Delta EFG}$ 重叠部分的面积 $S$ 与运动时间 $t$ 的函数图象大致是 $($ 　　 $)$

A．

B．

C．

D．

下列判断正确的是 $($ 　　 $)$

A．	$\frac{\sqrt{5}-1}{2}<0.5$
B．	若 $\mathit{ab}=0$ ，则 $a=b=0$
C．	$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$
D．	$3a$ 可以表示边长为 $a$ 的等边三角形的周长

将等腰直角三角形纸片和矩形纸片按如图方式叠放在起，若 $\angle 1=30°$ ，则 $\angle 2$ 的度数为 $($ 　　 $)$

A．

$10°$

B．

$15°$

C．

$20°$

D．

$30°$

如图，已知 $E$ ， $B$ ， $F$ ， $C$ 四点在一条直线上， $\mathit{EB}=\mathit{CF}$ ， $\angle A=\angle D$ ，添加以下条件之一，仍不能证明 $\mathit{\Delta ABC}\cong \mathit{\Delta DEF}$ 的是 $($ 　　 $)$

A．

$\angle E=\angle \mathit{ABC}$

B．

$\mathit{AB}=\mathit{DE}$

C．

$\mathit{AB}//\mathit{DE}$

D．

$\mathit{DF}//\mathit{AC}$

如图，有两张矩形纸片 $\mathit{ABCD}$ 和 $\mathit{EFGH}$ ， $\mathit{AB}=\mathit{EF}=2\mathit{cm}$ ， $\mathit{BC}=\mathit{FG}=8\mathit{cm}$ ．把纸片 $\mathit{ABCD}$ 交叉叠放在纸片 $\mathit{EFGH}$ 上，使重叠部分为平行四边形，且点 $D$ 与点 $G$ 重合．当两张纸片交叉所成的角 $\alpha$ 最小时， $\tan \alpha$ 等于 $($ 　　 $)$

A．

$\frac{1}{4}$

B．

$\frac{1}{2}$

C．

$\frac{8}{17}$

D．

$\frac{8}{15}$

如图，等边三角形 $\mathit{ABC}$ 的边长为8，以 $\mathit{BC}$ 上一点 $O$ 为圆心的圆分别与边 $\mathit{AB}$ ， $\mathit{AC}$ 相切，则 $\odot O$ 的半径为 $($ 　　 $)$

A．

$2\sqrt{3}$

B．

3

C．

4

D．

$4-\sqrt{3}$

下列长度的三条线段，能组成三角形的是 $($ 　　 $)$

A．

3，4，8

B．

5，6，10

C．

5，5，11

D．

5，6，11

如图1，长、宽均为3，高为8的长方体容器，放置在水平桌面上，里面盛有水，水面高为6，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图2是此时的示意图，则图2中水面高度为 $($ 　　 $)$

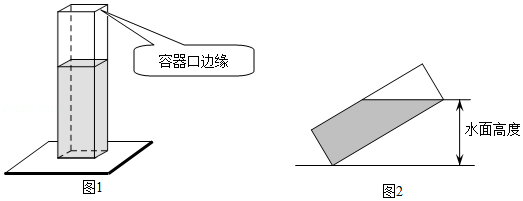
A．

$\frac{24}{5}$

B．

$\frac{32}{5}$

C．

$\frac{12\sqrt{34}}{17}$

D．

$\frac{20\sqrt{34}}{17}$

正方形 $\mathit{ABCD}$ 的边 $\mathit{AB}$ 上有一动点 $E$ ，以 $\mathit{EC}$ 为边作矩形 $\mathit{ECFG}$ ，且边 $\mathit{FG}$ 过点 $D$ ．在点 $E$ 从点 $A$ 移动到点 $B$ 的过程中，矩形 $\mathit{ECFG}$ 的面积 $($ 　　 $)$

A．

先变大后变小

B．

先变小后变大

C．

一直变大

D．

保持不变

如图， $\mathit{\Delta ABC}$ 内接于 $\odot O$ ， $\angle B=65°$ ， $\angle C=70°$ ．若 $\mathit{BC}=2\sqrt{2}$ ，则 $\stackrel{̂}{\mathit{BC}}$ 的长为 $($ 　　 $)$

A．

$\pi$

B．

$\sqrt{2}\pi$

C．

$2\pi$

D．

$2\sqrt{2}\pi$

如图，墙上钉着三根木条 $a$ ， $b$ ， $C$ ，量得 $\angle 1=70°$ ， $\angle 2=100°$ ，那么木条 $a$ ， $b$ 所在直线所夹的锐角是 $($ 　　 $)$

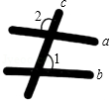
A．

$5°$

B．

$10°$

C．

$30°$

D．

$70°$

如图，取两根等宽的纸条折叠穿插，拉紧，可得边长为2的正六边形．则原来的纸带宽为 $($ 　　 $)$

A．

1

B．

$\sqrt{2}$

C．

$\sqrt{3}$

D．

2

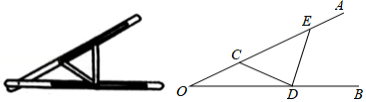
"三等分角"大约是在公元前五世纪由古希腊人提出来的，借助如图所示的"三等分角仪"能三等分任一角．这个三等分角仪由两根有槽的棒 $\mathit{OA}$ ， $\mathit{OB}$ 组成，两根棒在 $O$ 点相连并可绕 $O$ 转动、 $C$ 点固定， $\mathit{OC}=\mathit{CD}=\mathit{DE}$ ，点 $D$ 、 $E$ 可在槽中滑动．若 $\angle \mathit{BDE}=75°$ ，则 $\angle \mathit{CDE}$ 的度数是 $($ 　　 $)$

A．

$60°$

B．

$65°$

C．

$75°$

D．

$80°$

勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若知道图中阴影部分的面积，则一定能求出 $($ 　　 $)$

A．	直角三角形的面积
B．	最大正方形的面积
C．	较小两个正方形重叠部分的面积
D．	最大正方形与直角三角形的面积和

已知直线 $m//n$ ，将一块含 $45°$ 角的直角三角板 $\mathit{ABC}$ 按如图方式放置，其中斜边 $\mathit{BC}$ 与直线 $n$ 交于点 $D$ ．若 $\angle 1=25°$ ，则 $\angle 2$ 的度数为 $($ 　　 $)$

A．

$60°$

B．

$65°$

C．

$70°$

D．

$75°$