若长度分别为 ,3,5的三条线段能组成一个三角形,则 的值可以是
| A. |
1 |
B. |
2 |
C. |
3 |
D. |
8 |
在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长为1的小正方形拼成的图形, 是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点 的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知在四边形 中, , 平分 , , , ,则四边形 的面积是

| A. |
24 |
B. |
30 |
C. |
36 |
D. |
42 |
在 中,若一个内角等于另外两个内角的差,则
| A. |
必有一个内角等于 |
B. |
必有一个内角等于 |
| C. |
必有一个内角等于 |
D. |
必有一个内角等于 |
如图,在 中, , , 于点 , 于点 , .连接 ,将 沿直线 翻折至 所在的平面内,得 ,连接 .过点 作 交 于点 .则四边形 的周长为

| A. |
8 |
B. |
|
C. |
|
D. |
|
如图, 是 的直径, 是 的切线, 为切点,若 ,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, 是 边上的中点,连结 ,把 沿 翻折,得到 , 与 交于点 ,连结 ,若 , ,则点 到 的距离为

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 是 的直径, 是 的切线, 为切点, 与 交于点 ,连结 .若 ,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
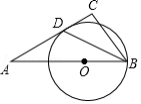
如图, 中, ,点 是边 上一点,以点 为圆心,以 为半径作圆, 恰好与 相切于点 ,连接 .若 平分 , ,则线段 的长是
| A. |
2 |
B. |
|
C. |
|
D. |
|
如图,以 为直径,点 为圆心的半圆经过点 ,若 ,则图中阴影部分的面积是

| A. |
|
B. |
|
C. |
|
D. |
|
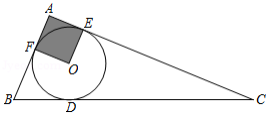
如图, 的内切圆 与 、 、 分别相切于点 、 、 ,且 , , ,则阴影部分(即四边形 的面积是
| A. |
4 |
B. |
6.25 |
C. |
7.5 |
D. |
9 |
如图,在正方形 中,连接 ,以点 为圆心,适当长为半径画弧,交 、 于点 , ,分别以 , 为圆心,大于 长的一半为半径画弧,两弧交于点 ,连结 并延长交 于点 ,再分别以 、 为圆心,以大于 长的一半为半径画弧,两弧交于点 , ,作直线 ,分别交 , , 于点 , , ,交 的延长线于点 ,连接 ,下列结论:① ,② ,③ ,④ .其中正确的是

| A. |
①②③ |
B. |
②③④ |
C. |
①③④ |
D. |
①②④ |
如图1,在矩形中,
为
边上一点
,
.将
沿
翻折得到△
,
的延长线交边
于点
,过点
作
交
于点
.
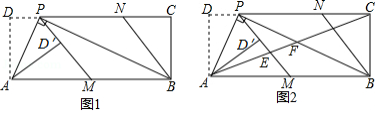
(1)求证:;
(2)请判断四边形的形状,并说明理由;
(3)如图2,连接,分别交
,
于点
,
.若
,求
的值.
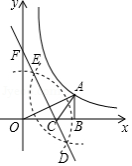
如图,点 在双曲线 上,过点 作 轴,垂足为点 ,分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 交 轴于点 ,交 轴于点 ,连接 .若 ,则 的值为
| A. |
2 |
B. |
|
C. |
|
D. |
|