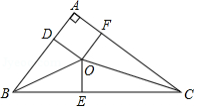
我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知 , , ,则正方形 的边长是
| A. |
|
B. |
2 |
C. |
|
D. |
4 |
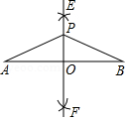
如图,分别以线段 的两端点 , 为圆心,大于 长为半径画弧,在线段 的两侧分别交于点 , ,作直线 交 于点 .在直线 上任取一点 (不与 重合),连接 , ,则下列结论不一定成立的是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,△ ,△ ,△ , 是分别以 , , , 为直角顶点,一条直角边在 轴正半轴上的等腰直角三角形,其斜边的中点 , , , , , , 均在反比例函数 的图象上.则 的值为

| A. |
|
B. |
6 |
C. |
|
D. |
|
如图,在平面直角坐标系中,等腰直角三角形 的顶点 、 分别在 轴、 轴的正半轴上, , 轴,点 在函数 的图象上,若 ,则 的值为

| A. |
1 |
B. |
|
C. |
|
D. |
2 |
如图,点 是正方形 的边 上一点,把 绕点 顺时针旋转 到 的位置.若四边形 的面积为20, ,则 的长为

| A. |
4 |
B. |
|
C. |
6 |
D. |
|
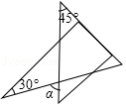
将一副直角三角板按如图所示的位置放置,使含 角的三角板的一条直角边和含 角的三角板的一条直角边放在同一条直线上,则 的度数是
| A. |
|
B. |
|
C. |
|
D. |
|
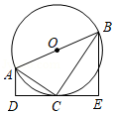
如图, 是 的直径,直线 与 相切于点 ,过 , 分别作 , ,垂足为点 , ,连接 , ,若 , ,则 的长为
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 与 轴交于点 , ,与 轴的正半轴交于点 .若 ,则点 的纵坐标为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,将 沿弦 折叠, 恰好经过圆心 ,若 的半径为3,则劣 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 是 的内接三角形, ,过点 的圆的切线交 于点 ,则 的度数为
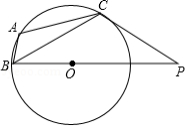
| A. |
|
B. |
|
C. |
|
D. |
|
如图,将一块三角尺的直角顶点放在直尺的一边上,当 时, 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,线段 经过 的圆心, , 分别与 相切于点 , .若 , ,则 的长度为

| A. |
|
B. |
|
C. |
|
D. |
|
如图, 是 上一点, 交 于点 , , ,若 , ,则 的长是

| A. |
0.5 |
B. |
1 |
C. |
1.5 |
D. |
2 |