如图,在正方形 中,点 , 分别在 , 上, , 与 相交于点 .下列结论:① 垂直平分 ;② ;③当 时, 为等边三角形;④当 时, .其中正确的是

A.①③B.②④C.①③④D.②③④
如图,在等边三角形
中,
,
与
相交于点
,
于点
,若
,则
的长为

A. B. C. D.4
我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里 米,则该沙田的面积为
A.7.5平方千米B.15平方千米C.75平方千米D.750平方千米
下列长度的三条线段,能组成三角形的是
A. , , B. , , C. , , D. , ,
如图, ,以点 为圆心,以任意长为半径作弧交 , 于 , 两点;分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;以 为端点作射线 ,在射线 上截取线段 ,则 点到 的距离为

A.6B.2C.3D.
如图,已知 是 的角平分线, 是 的垂直平分线, , ,则 的长为

A.6B.5C.4D.
如图示,若 内一点 满足 ,则点 为 的布洛卡点.三角形的布洛卡点 是法国数学家和数学教育家克洛尔 . . 于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡 重新发现,并用他的名字命名.问题:已知在等腰直角三角形 中, ,若点 为 的布洛卡点, ,则
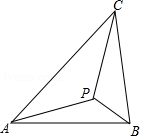
A.5B.4C. D.
如图,将正方形 折叠,使顶点 与 边上的一点 重合 不与端点 , 重合),折痕交 于点 ,交 于点 ,边 折叠后与边 交于点 .设正方形 的周长为 , 的周长为 ,则 的值为

A. B.
C. D.随 点位置的变化而变化
一个三角形的三个内角的度数之比为 ,则这个三角形一定是
A.锐角三角形B.直角三角形
C.钝角三角形D.等腰直角三角形
如图, , 分别是 的边 , 上的中点,如果 的周长是6,则 的周长是

A.6B.12C.18D.24