一个等腰三角形的边长是6,腰长是一元二次方程 的一根,则此三角形的周长是
A.12B.13C.14D.12或14
如图,正方形 中.点 , 分别在 , 上, 是等边三角形.连接 交 于点 .过点 作 于点 ,若 ,则

A.6B.4C.3D.2
如图,直角 中, ,点 是 的重心,连接 并延长交 于点 ,过点 作 交 于点 ,连接 交 于点 ,则 的值为

A. B. C. D.
如图, 过 对角线的交点 ,交 于 ,交 于 ,若 的周长为18, ,则四边形 的周长为

A.14B.13C.12D.10
已知抛物线 具有如下性质:该抛物线上任意一点到定点 的距离与到 轴的距离始终相等,如图,点 的坐标为 , , 是抛物线 上一个动点,则 周长的最小值是

A.3B.4C.5D.6
已知三角形的三边长分别为 、 、 ,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦 ,约公元50年)给出求其面积的海伦公式 ,其中 ;我国南宋时期数学家秦九韶(约 曾提出利用三角形的三边求其面积的秦九韶公式 ,若一个三角形的三边长分别为2,3,4,则其面积是
A. B. C. D.
如图, 为等边三角形 内的一点,且 到三个顶点 , , 的距离分别为3,4,5,则 的面积为
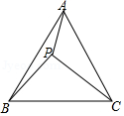
A. B. C. D.
如图,在 中, 平分 交 于点 ,过点 作 交 于点 ,且 平分 ,若 ,则 的长为

A.4B.6C. D.8