如图,在 中, , ,以点 为圆心, 长为半径画弧,交 于点 ,连接 ,则 的度数是
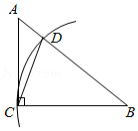
A. B. C. D.
如图, 和 都是等边三角形,且点 、 、 在一条直线上,连结 、 ,点 、 分别是线段 、 上的两点,且 , ,则 的形状是

A.等腰三角形B.直角三角形C.等边三角形D.不等边三角形
如图,要测定被池塘隔开的 , 两点的距离.可以在 外选一点 ,连接 , ,并分别找出它们的中点 , ,连接 .现测得 , , ,则

A. B. C. D.
如图,在 中,尺规作图如下:分别以点 ,点 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 ,交 于点 ,连接 ,则下列结论正确的是

A. 平分 B. 垂直平分 C. 垂直平分 D. 平分
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为 ,较短直角边长为 ,若 ,大正方形的面积为13,则小正方形的面积为

A.3B.4C.5D.6
如图,在 中, , , ,以点 为圆心, 长为半径作弧,交 于点 ;再分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于点 ,作射线 交 于点 ,则 的长为

A.5B.6C.7D.8
在平面直角坐标系 中,将一块含有 角的直角三角板如图放置,直角顶点 的坐标为 ,顶点 的坐标为 ,顶点 恰好落在第一象限的双曲线上,现将直角三角板沿 轴正方向平移,当顶点 恰好落在该双曲线上时停止运动,则此时点 的对应点 的坐标为

A. , B. C. , D.
如图, 是反比例函数 在第一象限内的图象上一点,以 为顶点作等边 ,使 落在 轴上,则 的面积为

A. B. C. D.
如图,在 中, ,以 的一边为边画等腰三角形,使得它的第三个顶点在 的其他边上,则可以画出的不同的等腰三角形的个数最多为

A.4B.5C.6D.7
如图, 是反比例函数 在第一象限内的图象上一点,以 为顶点作等边 ,使 落在 轴上,则 的面积为

A. B. C. D.
如图,在矩形 中, , 为 边的中点,将 绕点 顺时针旋转 ,点 的对应点为 ,点 的对应点为 ,过点 作 交 于点 ,连接 、 交于点 ,现有下列结论:
① ;
② ;
③ ;
④点 为 的外心.
其中正确的个数为

A.1个B.2个C.3个D.4个
如图,在正方形 中,点 是边 的中点,连接 、 ,分别交 、 于点 、 ,过点 作 交 的延长线于 ,下列结论:
① ,
② ,
③ ,
④若四边形 的面积为4,则该正方形 的面积为36,
⑤ .
其中正确的结论有

A.5个B.4个C.3个D.2个