如图,矩形 中, , ,点 在对角线 上,且 ,连接 并延长,交 的延长线于点 ,连接 ,则 的长为 .

等腰三角形的一边长是3,另两边的长是关于 的方程 的两个根,则 的值为
A.3B.4C.3或4D.7
如图,在 中,以 为直径的 交 于点 ,弦 交 于点 ,且 , , .
(1)求证: 是 的切线;
(2)求 的直径 的长度.
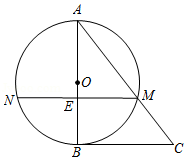
如图,在 中, , , 的半径为1,点 是 边上的动点,过点 作 的一条切线 (其中点 为切点),则线段 长度的最小值为 .

如图,在正方形 中,点 是 上一动点(不与 、 重合),对角线 、 相交于点 ,过点 分别作 、 的垂线,分别交 、 于点 、 ,交 、 于点 、 .下列结论:
① ;
② ;
③ ;
④ ;
⑤点 在 、 两点的连线上.
其中正确的是

A.①②③④B.①②③⑤C.①②③④⑤D.③④⑤
如图1,点 从 的顶点 出发,沿 匀速运动到点 ,图2是点 运动时线段 的长度 随时间 变化的关系图象,其中点 为曲线部分的最低点,则 的边 的长度为

A.12B.8C.10D.13
问题探究:
小红遇到这样一个问题:如图1, 中, , , 是中线,求 的取值范围.她的做法是:延长 到 ,使 ,连接 ,证明 ,经过推理和计算使问题得到解决.
请回答:(1)小红证明 的判定定理是: ;
(2) 的取值范围是 ;
方法运用:
(3)如图2, 是 的中线,在 上取一点 ,连结 并延长交 于点 ,使 ,求证: .
(4)如图3,在矩形 中, ,在 上取一点 ,以 为斜边作 ,且 ,点 是 的中点,连接 , ,求证: .

如图,在矩形 中, , .把 沿 折叠,使点 恰好落在 边上的 处,再将 绕点 顺时针旋转 ,得到△ ,使得 恰好经过 的中点 . 交 于点 ,连接 .有如下结论:① 的长度是 ;②弧 的长度是 ;③△ △ ;④△ .上述结论中,所有正确的序号是 .
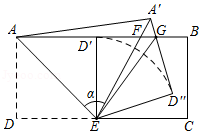
如图, 是 的直径, 和 是它的两条切线,过 上一点 作直线 ,分别交 、 于点 、 ,且 .
(1)求证:直线 是 的切线;
(2)求证: .
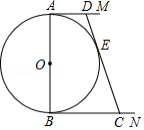
如图,过 对角线 与 的交点 作两条互相垂直的直线,分别交边 、 、 、 于点 、 、 、 .
(1)求证: ;
(2)顺次连接点 、 、 、 ,求证:四边形 是菱形.
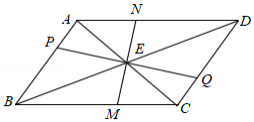
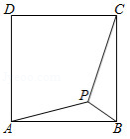
如图,点 是正方形 内一点,且点 到点 、 、 的距离分别为 、 、4,则正方形 的面积为 .
现有下列长度的五根木棒:3,5,8,10,13,从中任取三根,可以组成三角形的概率为 .