如图,△ 为等腰直角三角形, ,以斜边 为直角边作等腰直角三角形 ,再以 为直角边作等腰直角三角形 , ,按此规律作下去,则 的长度为
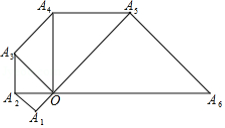
A. B. C. D.
如图1,在 中, , ,点 , 分别在边 , 上,且 ,连接 .现将 绕点 顺时针方向旋转,旋转角为 ,如图2,连接 , , .
(1)当 时,求证: ;
(2)如图3,当 时,延长 交 于点 ,求证: 垂直平分 ;
(3)在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.

如图,在 中, , , 垂直平分 ,垂足为 ,交 于点 .按以下步骤作图:①以点 为圆心,以适当的长为半径作弧,分别交边 , 于点 , ;②分别以点 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;③作射线 .若 与 的夹角为 ,则 .

如图, 的外角 的平分线与它的外接圆相交于点 ,连接 , ,过点 作 ,交 于点 .
求证:(1) ;
(2) 为 的切线.

如图,四边形 是一张正方形纸片,其面积为 .分别在边 , , , 上顺次截取 ,连接 , , , .分别以 , , , 为轴将纸片向内翻折,得到四边形 .若四边形 的面积为 ,则 .

如图,在 中,对角线 , , , 为 的中点, 为边 上一点,直线 交 于点 ,连结 , .下列结论不成立的是
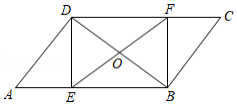
A.四边形 为平行四边形
B.若 ,则四边形 为矩形
C.若 ,则四边形 为菱形
D.若 ,则四边形 为正方形
七巧板是大家熟悉的一种益智玩具.用七巧板能拼出许多有趣的图案.小李将一块等腰直角三角形硬纸板(如图① 切割七块,正好制成一副七巧板(如图② .已知 ,则图中阴影部分的面积为
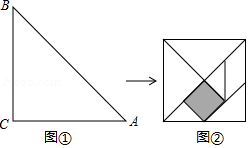
A. B. C. D.
小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形, 与 恰好为对顶角, ,连接 , ,点 是线段 上一点.
探究发现:
(1)当点 为线段 的中点时,连接 (如图(2) ,小明经过探究,得到结论: .你认为此结论是否成立? .(填"是"或"否"
拓展延伸:
(2)将(1)中的条件与结论互换,即: ,则点 为线段 的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
问题解决:
(3)若 , ,求 的长.

若 和 均为等腰三角形,且 .
(1)如图(1),点 是 的中点,判定四边形 的形状,并说明理由;
(2)如图(2),若点 是 的中点,连接 并延长至点 ,使 .
求证:① ,
② .

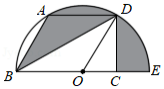
如图,点 是半圆圆心, 是半圆的直径,点 , 在半圆上,且 , , ,过点 作 于点 ,则阴影部分的面积是 .
如图,点 , 的坐标分别为 , ,点 为坐标平面内一点, ,点 为线段 的中点,连接 ,则 的最大值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,矩形 中, , 相交于点 ,过点 作 交 于点 ,交 于点 ,过点 作 交 于点 ,交 于点 ,连接 , .则下列结论:
① ;
② ;
③ ;
④当 时,四边形 是菱形.
其中,正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
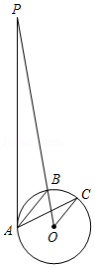
如图, 是 的切线,点 为切点, 交 于点 , ,点 在 上, .则 等于
| A. |
|
B. |
|
C. |
|
D. |
|