二次函数 的图象如图所示,下列结论: ; ; ; ,其中正确的个数是( )

A.1B.2C.3D.4
如图,在平面直角坐标系中,抛物线 经过点(﹣1,8)并与x轴交于点A,B两点,且点B坐标为(3,0).
(1)求抛物线的解析式;
(2)若抛物线与y轴交于点C,顶点为点P,求△CPB的面积.
注:抛物线 的顶点坐标是
将抛物线 向下平移8个单位长度后与x轴的两个交点之间的距离为( )
A.4B.6C.8D.10
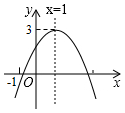
如图,抛物线 y= ax 2+ bx+ c( a≠0)的对称轴为直线 x=1,与 x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4 ac< b 2;
②方程 ax 2+ bx+ c=0的两个根是 x 1=﹣1, x 2=3;
③3 a+ c>0
④当 y>0时, x的取值范围是﹣1≤ x<3
⑤当 x<0时, y随 x增大而增大
其中结论正确的个数是( )

| A. |
4个 |
B. |
3个 |
C. |
2个 |
D. |
1个 |
如图是抛物线 的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
① ;
② ;
③ ;
④一元二次方程 有两个不相等的实数根.
其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
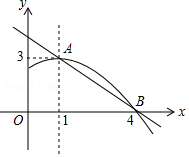
如图是抛物线 的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线 与抛物线交于A,B两点,下列结论:
① ;②方程 有两个相等的实数根;③抛物线与x轴的另一个交点是(﹣1,0);④当 时,有 ;⑤ ,其中正确的结论是 .(只填写序号)
二次函数 y= ax 2+ bx+ c( a≠0)的图象如图所示,下列结论正确是( )
| A. |
abc>0 |
| B. |
2a+b<0 |
| C. |
3a+c<0 |
| D. |
ax 2+bx+c﹣3=0有两个不相等的实数根 |
已知抛物线 y= x 2+ mx﹣2 m﹣4( m>0).
(1)证明:该抛物线与 x轴总有两个不同的交点;
(2)设该抛物线与 x轴的两个交点分别为 A, B(点 A在点 B的右侧),与 y轴交于点 C, A, B, C三点都在⊙ P上.
①试判断:不论 m取任何正数,⊙ P是否经过 y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;
②若点 C关于直线 x=﹣ 的对称点为点 E,点 D(0,1),连接 BE, BD, DE,△ BDE的周长记为 l,⊙ P的半径记为 r,求 的值.
已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b.
(Ⅰ)求抛物线顶点Q的坐标(用含a的代数式表示);
(Ⅱ)说明直线与抛物线有两个交点;
(Ⅲ)直线与抛物线的另一个交点记为N.
(ⅰ)若 ,求线段MN长度的取值范围;
(ⅱ)求△QMN面积的最小值.
二次函数y=ax2+bx+c(a≠0)和正比例函数 的图象如图所示,则方程 的两根之和( )

A.大于0B.等于0C.小于0D.不能确定
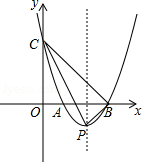
已知直线y=﹣ x+3与坐标轴分别交于点A,B,点P在抛物线 上,能使△ABP为等腰三角形的点P的个数有( )
A.3个B.4个C.5个D.6个
如图,抛物线 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )

A.(4,3)B.(5, )C.(4, )D.(5,3)