模具厂计划生产面积为4,周长为的矩形模具.对于
的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为,
,由矩形的面积为4,得
,即
;由周长为
,得
,即
.满足要求的
应是两个函数图象在第 一 象限内交点的坐标.
(2)画出函数图象
函数的图象如图所示,而函数
的图象可由直线
平移得到.请在同一直角坐标系中直接画出直线
.
(3)平移直线,观察函数图象
①当直线平移到与函数的图象有唯一交点
时,周长
的值为 ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长的取值范围为 .

反比例函数 为常数,且 的图象经过点 、 .
(1)求反比例函数的解析式及 点的坐标;
(2)在 轴上找一点 ,使 的值最小,求满足条件的点 的坐标.

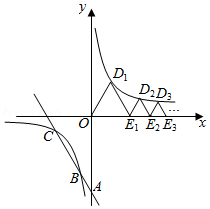
如图,直线 与 轴交于点 ,与双曲线 在第三象限交于 、 两点,且 .下列等边三角形△ ,△ ,△ , 的边 , , , 在 轴上,顶点 , , , 在该双曲线第一象限的分支上,则 ,前25个等边三角形的周长之和为 .
关于反比例函数 ,下列说法正确的是
| A. |
函数图象经过点 |
B. |
函数图象位于第一、三象限 |
| C. |
当 时, 随 的增大而减小 |
D. |
当 时, |
对于反比例函数 ,下列说法不正确的是
A.图象分布在第二、四象限
B.当 时, 随 的增大而增大
C.图象经过点
D.若点 , , , 都在图象上,且 ,则
如图,已知反比例函数 与正比例函数 的图象交于 , 两点.
(1)求该反比例函数的表达式;
(2)若点 在 轴上,且 的面积为3,求点 的坐标.

在平面直角坐标系中,对于不在坐标轴上的任意一点 ,我们把点 , 称为点 的"倒数点".如图,矩形 的顶点 为 ,顶点 在 轴上,函数 的图象与 交于点 .若点 是点 的"倒数点",且点 在矩形 的一边上,则 的面积为 .

已知三个点 , , , , , 在反比例函数 的图象上,其中 ,下列结论中正确的是
| A. |
|
B. |
|
C. |
|
D. |
|
已知反比例函数 的图象经过点 .
(1)求该反比例函数的表达式;
(2)如图,在反比例函数 的图象上点 的右侧取点 ,过点 作 轴的垂线交 轴于点 ,过点 作 轴的垂线交直线 于点 .
①过点 ,点 分别作 轴, 轴的垂线,两线相交于点 ,求证: , , 三点共线;
②若 ,求证: .
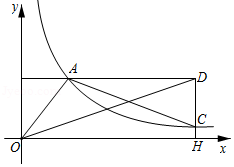
如图,在平面直角坐标系中,一次函数 的图象与 轴相交于点 ,与反比例函数 在第一象限内的图象相交于点 ,过点 作 轴于点 .
(1)求反比例函数的解析式;
(2)求 的面积.
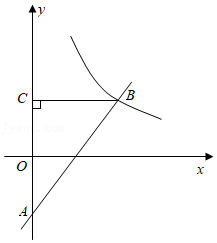
如图,在平面直角坐标系中,矩形 的对角线 的中点与坐标原点重合,点 是 轴上一点,连接 .若 平分 ,反比例函数 的图象经过 上的两点 , ,且 , 的面积为18,则 的值为

A.6B.12C.18D.24
探究函数 与 的相关性质.
(1)小聪同学对函数 进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
(2)请用配方法求函数 的最小值;
(3)猜想函数 的最小值为 .

如图,在平面直角坐标系中,等边 和菱形 的边 , 都在 轴上,点 在 边上, ,反比例函数 的图象经过点 ,则 的值为 .
