第一次"龟兔赛跑",兔子因为在途中睡觉而输掉比赛,很不服气,决定与乌龟再比一次,并且骄傲地说,这次我一定不睡觉,让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛,则下列函数图象可以体现这次比赛过程的是
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在 中, , , 是 上的一点(不与 、 重合), ,垂足是点 ,设 ,四边形 的周长为 ,则下列图象能大致反映 与 之间的函数关系的是

A.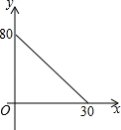 B.
B.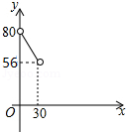
C.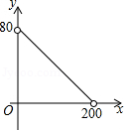 D.
D.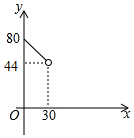
从某容器口以均匀地速度注入酒精,若液面高度 随时间 的变化情况如图所示,则对应容器的形状为
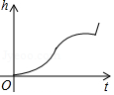
| A. |
|
B. |
|
C. |
|
D. |
|
定义 表示不超过实数 的最大整数,如 , , .函数 的图象如图所示,则方程 的解为
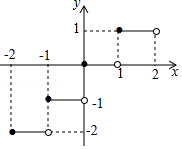
A.0或 B.0或1C.1或 D. 或
均匀地向一个容器内注水,在注满水的过程中,水面的高度 与时间 的函数关系如图所示,则该容器是下列四个中的

| A. |
|
B. |
|
C. |
|
D. |
|
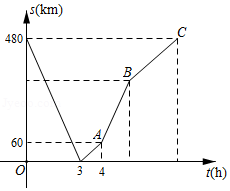
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续行驶乙地,两车到达各地终点后停止,两车之间的距离 与慢车行驶的时间 之间的关系如图:
(1)快车的速度为 , 点的坐标为 .
(2)慢车出发多少小时后,两车相距 .
如图1,在四边形中,
,
,直线
.当直线
沿射线
方向,从点
开始向右平移时,直线
与四边形
的边分别相交于点
、
.设直线
向右平移的距离为
,线段
的长为
,且
与
的函数关系如图2所示,则四边形
的周长是 .
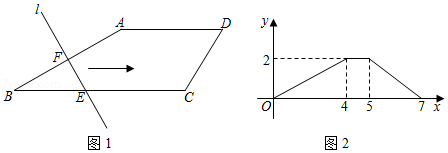
小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程 与时间 的大致图象是
A.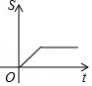 B.
B.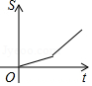
C. D.
D.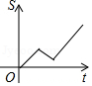
回顾初中阶段函数的学习过程,从函数解析式到函数图象,再利用函数图象研究函数的性质,这种研究方法主要体现的数学思想是
A.数形结合B.类比C.演绎D.公理化
小明从家出发沿笔直的公路去图书馆,在图书馆阅读书报后按原路回到家.如图,反映了小明离家的距离 (单位: 与时间 (单位: 之间的对应关系.下列描述错误的是

| A. |
小明家距图书馆 |
| B. |
小明在图书馆阅读时间为 |
| C. |
小明在图书馆阅读书报和往返总时间不足 |
| D. |
小明去图书馆的速度比回家时的速度快 |
已知 , 两地相距 ,甲、乙两人沿同一条公路从 地出发到 地,甲骑自行车匀速行驶 到达,乙骑摩托车,比甲迟 出发,行至 处追上甲,停留半小时后继续以原速行驶.他们离开 地的路程 与甲行驶时间 的函数图象如图所示.当乙再次追上甲时距离 地

| A. |
|
B. |
|
C. |
|
D. |
|
一对变量满足如图的函数关系.设计以下问题情境:
①小明从家骑车以600米 分的速度匀速骑了2.5分钟,在原地停留了2分钟,然后以1000米 分的速度匀速骑回家.设所用时间为 分钟,离家的距离为 千米;
②有一个容积为1.5升的开口空瓶,小张以0.6升 秒的速度匀速向这个空瓶注水,注满后停止,等2秒后,再以1升 秒的速度匀速倒空瓶中的水.设所用时间为 秒,瓶内水的体积为 升;
③在矩形 中, , ,点 从点 出发.沿 路线运动至点 停止.设点 的运动路程为 , 的面积为 .
其中,符合图中函数关系的情境个数为

| A. |
3 |
B. |
2 |
C. |
1 |
D. |
0 |
甲、乙两地相距 ,一辆汽车上午 从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了 ,并继续匀速行驶至乙地,汽车行驶的路程 与时间 之间的函数关系如图所示,该车到达乙地的时间是当天上午

A. B. C. D.
“龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终贏得比赛,下列函数图象可以体现这一故事过程的是
A.
B.
C.
D.