将平行四边形 放置在如图所示的平面直角坐标系中,点 为坐标原点.若点 的坐标为 ,点 的坐标为 ,则点 的坐标为 .
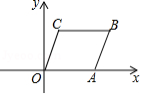
如图,在直角坐标系 中,矩形 的顶点 、 分别在 轴和 轴正半轴上,点 的坐标是 ,点 是 边上一动点(不与点 、点 重合),连接 、 ,过点 作射线 交 的延长线于点 ,交 边于点 ,且 ,令 , .
(1)当 为何值时, ?
(2)求 与 的函数关系式,并写出 的取值范围;
(3)在点 的运动过程中,是否存在 ,使 的面积与 的面积之和等于 的面积?若存在,请求 的值;若不存在,请说明理由.

如图,点 , , , 均在坐标轴上,且 , ,若点 , 的坐标分别为 , ,则点 的坐标为 .

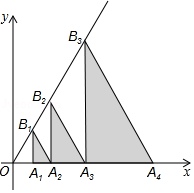
如图, 、 、 、… 都是等边三角形,其中 、 、… 都与x轴垂直,点A1、A2、…An都在x轴上,点B1、B2、…Bn都在直线 上,已知 ,则点A2016的坐标为 .
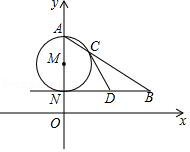
如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
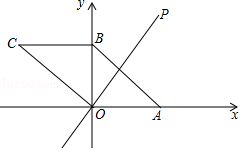
如图,在平面直角坐标系xOy中,▱ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线 上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与▱ABCO的边相切时,P点的坐标为 .
如图,若菱形 ABCD的顶点 A, B的坐标分别为(3,0),(﹣2,0),点 D在 y轴上,则点 C的坐标是 .

已知正方形的对称中心在坐标原点,顶点 A、 B、 C、 D按逆时针依次排列,若 A点的坐标为(2, ),则 B点与 D点的坐标分别为( )
| A. |
(﹣2, ),(2,﹣ ) |
B. |
(﹣ ,2),( ,﹣2) |
| C. |
(﹣ ,2),(2,﹣ ) |
D. |
(- , )( , ) |
如图,在平面直角坐标系中,已知 A(﹣1,0), B(0,2),将△ ABO沿直线 AB翻折后得到△ ABC,若反比例函数 y= ( x<0)的图象经过点 C,则 k= .

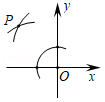
如图,在平面直角坐标系中,以 O为圆心,适当长为半径画弧,交 x轴于点 M,交 y轴于点 N,再分别以点 M, N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点 P,若点 P的坐标为(3 a, b+1),则 a与 b的数量关系为( )
| A. |
3a=2b |
B. |
3a=b+1 |
C. |
3a+b﹣1=0 |
D. |
3a=﹣b﹣1 |
平面直角坐标系中,已知 .若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5B.6C.7D.8