探索与发现:下面是用分数(数字表示面积)砌成的“分数墙”,则整面“分数墙”的总面积是 .

将从1开始的连续自然数按以下规律排列:
第1行 |
1 |
||||||||
第2行 |
2 |
3 |
4 |
||||||
第3行 |
9 |
8 |
7 |
6 |
5 |
||||
第4行 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
||
第5行 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
则2017在第 行.
数轴上,
两点的距离为4,一动点
从点
出发,按以下规律跳动:第1次跳动到
的中点
处,第2次从
点跳动到
的中点
处,第3次从
点跳动到
的中点
处,按照这样的规律继续跳动到点
,
,
,
,
.
,
是整数)处,那么线段
的长度为 .

如图所示,是一个运算程序示意图.若第一次输入 的值为125,则第2018次输出的结果是 .

观察下列一组数:
,
,
,
,
,
,
它们是按一定规律排列的,请利用其中规律,写出第个数
(用含
的式子表示)
如图所示,下列各三角形中的三个数之间均有相同的规律,根据此规律,当图中 时,正整数 的值为 .

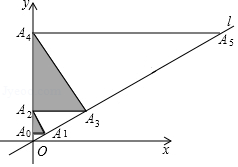
如图,过点 作 轴的垂线交直线 于点 ,过点 作直线 的垂线,交 轴于点 ,过点 作 轴的垂线交直线 于点 , ,这样依次下去,得到△ ,△ ,△ , ,其面积分别记为 , , , ,则 为
| A. |
|
B. |
|
C. |
|
D. |
|
生活中常用的十进制是用 这十个数字来表示数,满十进一,例: , ;计算机也常用十六进制来表示字符代码,它是用 来表示 ,满十六进一,它与十进制对应的数如表:
| 十进制 |
0 |
1 |
2 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
| 十六进制 |
0 |
1 |
2 |
|
8 |
9 |
|
|
|
|
|
|
10 |
11 |
|
例:十六进制 对应十进制的数为 , 对应十进制的数为 ,那么十六进制中 对应十进制的数为
| A. |
28 |
B. |
62 |
C. |
238 |
D. |
334 |
已知 为实数,规定运算: , , , , , .按上述方法计算:当 时, 的值等于
| A. |
|
B. |
|
C. |
|
D. |
|
观察下列各式的规律:
① ;② ;③ .
请按以上规律写出第4个算式 .
用含有字母的式子表示第 个算式为 .
如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第9行从左至右第5个数是
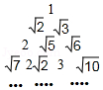
A. B. C. D.
在一列数: , , , , 中, , ,从第三个数开始,每一个数都等于它前两个数之积的个位数字,则这一列数中的第2017个数是
A.1B.3C.7D.9