初中数学计算器—基础知识解答题

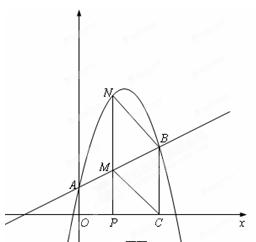
如图，在直角坐标平面内，函数（，是常数）
的图象经过，，其中．过点作轴垂线，
垂足为，过点作轴垂线，垂足为，连结，，．

若的面积为4，求点的坐标；
若，当时，求直线的函数的解析式．

．矩形的长和宽分别是4cm, 3cm ，如果将长和宽都增加x cm ，那么面积增加ycm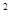
求y与x之间的关系式.
求当边长增加多少时，面积增加8 cm

随着大陆惠及台胞政策措施的落实，台湾水果进入了大陆市场。一水果经销商购进了A，B两种台湾水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售。预计每箱水果的盈利情况如下表：

有两种配货方案（整箱配货）：
方案一：甲、乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱；
方案二：按照甲、乙两店盈利相同配货，其中A种水果甲店_________箱，乙店__________箱；B种水果甲店_________箱，乙店__________箱.
如果按照方案一配货，请你计算出经销商能盈利多少元？
请你将方案二填写完整（只填写一种情况即可），并根据你填写的方案二与方案一作比较，哪种方案盈利较多？
在甲、乙两店各配货10箱，且保证乙店盈利不小于100元的条件下，请你设计出使水果经销商盈利最大的配货方案，并求出最大盈利为多少？

某教师的月工资数与工作的年数如下表所示（工资单位：元）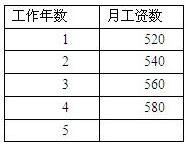

（1）填出第5年他的月工资数；
（2）用含n的代数式表示他第n年的月工资数；
（3）用（2）的代数式求该教师工作第17年的
工资数．

某城市出租汽车收费标准为：4km以内（含4km）收费10元；超出4km的部分，每千米收费1.4元．
写出车费y元与行驶路程x千米之间的函数关系式（x≥4）
某人乘出租汽车行驶了5km，应付多少车费？
若某人付了17元车费，那么出租车行驶了多远

直线y=－x+6与坐标轴分别交于A、B两点，动点P、Q同时从O点匀速出发，同时到达A点时运动停止．点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O→B→A运动．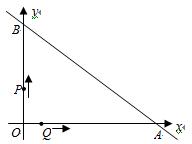

直接写出A、B两点的坐标；
设点Q的运动时间为t秒，△OPQ的面积为S，求出S与t之间的函数关系式；
当s= 时，求出点P的坐标，并直接写出以点O、P、Q为顶点的平行四边形的
第四个顶点M的坐标．

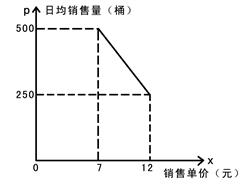
无锡市南长区某桶装水经营部每天的房租、人员工资等固定成本为250元，每桶水的进价是5元，规定销售单价不得高于12元/桶，也不得低于7元/桶，调查发现日均销售量p(桶)与销售单价x（元）的函数图象如图所示．
求日均销售量p（桶）与销售单价x（元）的函数关系；
若该经营部希望日均获利1350元，请你根据以上信息，就该桶装水的销售单价或销售数量，提出一个用一元二次方程解决的问题，并写出解答过程．

一根祝寿蜡烛长85cm,点燃时每小时缩短5cm。
请写出点燃后蜡烛的长y(cm)与蜡烛燃烧时间t（h）之间的函数关系式；
该蜡烛可点燃多长时间？

如图①，一条笔直的公路上有A、B、C 三地，B、C 两地相距150千米，甲、乙两辆汽车分别从
B、C两地同时出发，沿公路匀速相向而行，分别驶往C、B 两地．甲、乙两车到A地的距离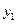
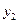、（千米）与行驶时间x（时）的关系如图②所示．
根据图象②进行以下探究：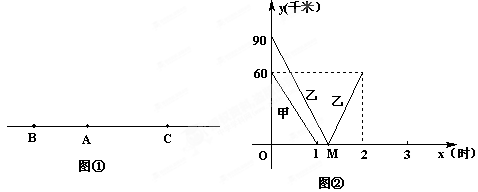

求图中②M点的坐标，并解释该点的实际意义．
在图②中补全甲车的函数图象，求甲车到A地的距离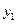与行驶时间x的函数关系式．
A地设有指挥中心，指挥中心及两车都配有对讲机，两部对讲机在15千米之内（含15千米）时能够互相通话，求两车可以同时与指挥中心用对讲机通话的时间．

如图1，已知抛物线的顶点为，且经过原点，与轴的另一个交点为．
求抛物线的解析式；
若点在抛物线的对称轴上，点在抛物线上，且以、、、四点为顶点的四边形为平行四边形，求点的坐标；
连接、，如图2，在轴下方的抛物线上是否存在点，使得 与相似？若存在，求出点的坐标；若不存在，说明理由．

如图，在平面直角坐标系中，点A、B、C、P的坐标分别为（0，1）、
（－1，0）、（1，0）、（－1，－1）。
求经过A、B、C三点的抛物线的表达式；
以P为位似中心，将△ABC放大，使得放大后的△A₁B₁C₁与△OAB对应线段的比为3：1，请在右图网格中画出放大后的△A₁B₁C₁；（所画△A₁B₁C₁与△ABC在点P同侧）；
经过A₁、B₁、C₁三点的抛物线能否由（1）中的抛物线平移得到？请说明理由。

深圳大运会期间，某宾馆有若干间住房，住宿记录提供了如下信
息：①7月20日全部住满，一天住宿费收入为3600元；②7月21日有10间房空着，一天住宿费收入为2800元；③该宾馆每间房每天收费标准相同。
求该宾馆共有多少间住房，每间住房每天收费多少元？
通过市场调查发现，每个住房每天的定价每增加10元，就会有一个房间空闲；己知该宾馆空闲房间每天每间费用10元，有游客居住房间每天每间再增加20元的其他费用，问房价定为多少元时，该宾馆一天的利润最大？

如图，在平面直角坐标系中，Rt△OAB的直角边OA在x轴的正半轴上，点B在第象限，将△OAB绕点O按逆时针方向旋转至△OA′B′，使点B的对应点B′落在y轴的正半轴上，已知OB=2，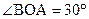

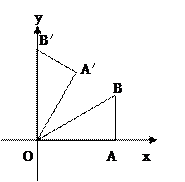
求点B和点A′的坐标；
求经过点B和点B′的直线所对应的一次函数解析式，并判断点A是否在直线BB′上。

如图，抛物线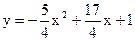与y轴交于A点，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C(3，0).
求直线AB的函数关系式；
动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N. 设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并写出t的取值范围；
设在（2）的条件下（不考虑点P与点O，点C重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平行四边形？问对于所求的t值，平行四边形BCMN是否菱形？请说明理由.

如图，在平面直角坐标系中有一矩形ABCO，B点的坐标为（12，6），点C、A在坐标轴上．⊙A、⊙P的半径均为1，点P从点C开始在线段CO上以1单位/秒的速度向左运动，运动到点O处停止．与此同时，⊙A的半径每秒钟增大2个单位，当点P停止运动时，⊙A的半径也停止变化．设点P运动的时间为t秒．
在0＜t＜12时，设△OAP的面积为s，试求s与t的函数关系式．并求出当t为何值时，s为矩形ABCO面积的；
在点P的运动过程中，是否存在某一时刻，⊙A与⊙P相切，若存在求出点P的坐标，若不存在，说明理由．