在平面直角坐标系中,已知△ABC三个顶点的坐标分别为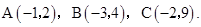
画出△ABC,并求出AC所在直线的解析式。
画出△ABC绕点A顺时针旋转
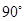 后得到的△A1B1C1,并求出△ABC在上述旋转过程中扫过的面积。
后得到的△A1B1C1,并求出△ABC在上述旋转过程中扫过的面积。
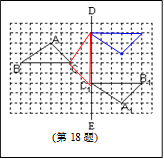
在如图的方格纸中,每个小正方形的边长都为l. 画出将△A1B1C1,沿直线DE方向向上平移5格得到的△A2B2C2;
要使△A2B2C2与△CC1C2重合,则△A2B2C2绕点C2顺时针方向旋转,至少要旋转多少度?(直接写出答案)
在条件(2)中,计算△A2B2C2 计扫过的面积。


如图,两摞相同规格的饭碗整齐地叠放在桌面上,请根据图中给的数据信息,解答下列问题:

求整齐摆放在桌面上饭碗的高度y(cm)与饭碗数x(个)之间的一次函数解析式
把这两摞饭碗整齐地摆成一摞时,这摞饭碗的高度是多少?
血橙以果肉酷似鲜血的颜色而得名,它本质上属脐橙类,现在已经开发出多种品种,果实一般在1月下旬成熟。由于果农在生产实践中积累了丰富的管理经验,大多采取了留树保鲜技术措施,将鲜果供应期拉长到了5月初。重庆市万州区晚熟柑橘以血橙为主,其中沙河街孙家村是万州血橙老产区,主要销售市场是成都、重庆市区、万州城区。据以往经验,孙家村上半年1~5月血橙的售价 (元/千克)与月份
(元/千克)与月份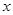 之间满足一次函数关系
之间满足一次函数关系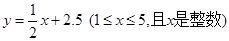 。其月销售量
。其月销售量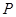 (千克)与月份
(千克)与月份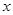 之间的相关数据如下表:
之间的相关数据如下表:
月份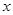 |
1月 |
2月 |
3月 |
4月 |
5月 |
销售量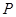 (千克) (千克) |
70000 |
65000 |
60000 |
55000 |
50000 |
请观察题中的表格,用所学过的一次函数,反比例函数或二次函数的有关知识,求月销售量
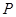 (千克)与月份
(千克)与月份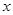 之间的函数关系式
之间的函数关系式血橙在上半年1~5月的哪个月出售,可使销售金额
 (元)最大?最大金额是多少元?
(元)最大?最大金额是多少元?由于气候适宜以及保鲜技术的提高,预计该产区今年5月将收获60000千克的血橙,并按(2)问中获得最大销售金额时的销售量售出新鲜血橙。剩下的血橙的果肉与石榴、白糖按5:2:1的比例制成“石榴·血橙白茶果冻”出售(以下简称“果冻”,制作过程中的损耗忽略不计),已知平均每千克的血橙含0.8千克的果肉。产区生产商最初将每千克果冻的批发价定为26元,超市的零售价比批发价高
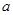 %,当销售了这批果冻的四分之三后,考虑到制作和营运成本的提高,生产商将批发价提高了
%,当销售了这批果冻的四分之三后,考虑到制作和营运成本的提高,生产商将批发价提高了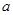 %,超市的零售价也跟着在此批发价的基础上提高了
%,超市的零售价也跟着在此批发价的基础上提高了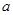 %,最后该产区将这批果冻在超市全部出售后的销售总额达到了390000元。求
%,最后该产区将这批果冻在超市全部出售后的销售总额达到了390000元。求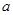 的值。(结果保留整数)
的值。(结果保留整数)
(参考数据: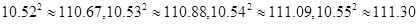 )
)
已知直线y = x+m与x轴、y轴分别交于点A、B,与双曲线y
= x+m与x轴、y轴分别交于点A、B,与双曲线y =
=  分别交于点C、D,且点C的坐标为(-1,2).
分别交于点C、D,且点C的坐标为(-1,2).分别求出直线AB及双曲线的函数表达式;
利用图像直接写出:当x在什么范围内取值时y
 >y
>y
(本题9分)如图,四边形ABCD.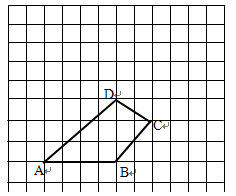
(1)建立以点B为原点,AB边所在直线为x轴的直角坐标系,并写出点A、B、C、D的坐标。
(2)求出四边形ABCD的面积。
(3)请画出将四边形ABCD向上平移5格,再向左平移2格后所得的四边形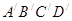
如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=-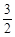 x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.若直线y=-
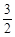 x+b平分矩形OABC的面积,求b的值;
x+b平分矩形OABC的面积,求b的值;在(1)的条件下,当直线y=-
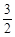 x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;在(1)的条件下,将矩形OABC沿DE折叠,若点O落在边BC上,求出该点坐标;若不在边BC上,求将(1)中的直线沿y轴怎样平移,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上
如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
请用含t的代数式表示出点D的坐标;
求t为何值时,△DPA的面积最大,最大为多少
在点P从O向A运动的过程中,△DPA
 能否成为直角三角形?若能,求t的值.
能否成为直角三角形?若能,求t的值.
若不能,请说明理 由;
由;请直接写出随着点P的运动,点D运动路线的
 长.
长.
夏天容易 发生腹泻等肠道疾病,某市医药公司的甲、乙两仓库分别存有医治腹泻的药品80箱和70箱,现需要将库存的药品调往A地100箱和B地50箱。已知从甲、乙两仓库运送药品到两地的费用(元/箱)如下表所示:
发生腹泻等肠道疾病,某市医药公司的甲、乙两仓库分别存有医治腹泻的药品80箱和70箱,现需要将库存的药品调往A地100箱和B地50箱。已知从甲、乙两仓库运送药品到两地的费用(元/箱)如下表所示: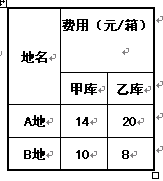
设从甲仓库运送到A地的药品为
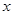 箱,求总费用
箱,求总费用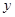 (元)与
(元)与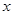 (箱)之间的函数关系式,并写出
(箱)之间的函数关系式,并写出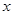 的取值范围
的取值范围求出最低费用,并说明总费用最低时的调配方案
直线 =
= (k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别
(k≠0)与坐标轴分别交于A、B两点,OA、OB的长分别
是方程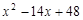 =0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每
=0的两根(OA>OB).动点P从O点出发,沿路线O→B→A以每
秒1个单位长度的速度运动,到达A点时运动停止.直接写出A、B两点的坐标;
设点P的运动时间为t(秒),△OPA的面积为S,求S与t之间的函数关系式;
当S=12时,求出点P的坐标,此时,在坐标轴上是否存在点M,使以O、A、
P、M为顶点的四边形是梯形?若存在,请直接写出点M的坐标;若不存在,请说明理由.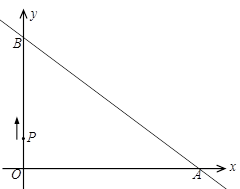
某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的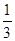 .
.求y与x之间的函数关系式;
由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
温州市有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售。设
 天后每千克该野生菌的市场价格为
天后每千克该野生菌的市场价格为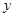 元,试写出
元,试写出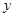 与
与 之间的函数关系式;
之间的函数关系式;若存放
 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为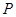 元,试写出
元,试写出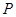 与
与 之间的函数关系式;
之间的函数关系式;李经理将这批野生菌存放多少天后出售可获得最大利润
 元?
元?
(利润=销售总额-收购成本-各种费用)
如图,在直角坐标平面内,函数 (
( ,
, 是常数)
是常数)
的图象经过 ,
, ,其中
,其中 .过点
.过点 作
作 轴垂线,
轴垂线,
垂足为 ,过点
,过点 作
作 轴垂线,垂足为
轴垂线,垂足为 ,连结
,连结 ,
, ,
, .
.
若
 的面积为4,求点
的面积为4,求点 的坐标;
的坐标;若
 ,当
,当 时,求直线
时,求直线 的函数的解析式.
的函数的解析式.